Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.4 (exercícios de compreensão) - Ex. 5
Em cada parte, determine o valor exato sem utilizar recursos computacionais
Passo 1
Fala povo, tudo certo? Ó só, pra gente matar essa questão bem rapidinho, vamos pensar o seguinte, como o enunciado fala tudo sobre arco de funções trigonométricas, se a gente lembrar por exemplo que:
Significa que é o arco cujo seno é , podemos reescrever todas as letras do enunciado:
Para:
Basicamente o que fizemos foi usar a função inversa das funções arco. Como as funções arco já são as inversas trigonométricas, voltamos pra elas. Bacana, não? Agora como temos funções iguais se igualando, é tentador pra gente responder:
O que não é inteiramente errado, mas como as funções trigonométricas são funções cíclicas, vamos ver com mais calma caso a caso, ok?! Em todos eles vamos precisar considerar o círculo trigonométrico:
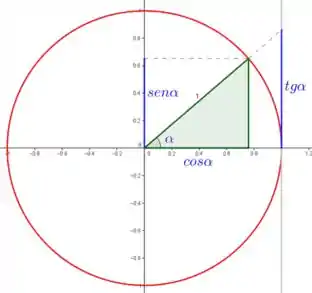
Passo 2
Letra a)
Show galera, olhando com carinho pro círculo trigonométrico, vemos que, pra ângulos genéricos , tal que:
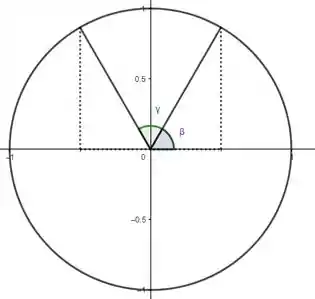
Vai ser válido que:
Portanto, como queremos:
Não basta respondermos porque, escolhendo , a escolha de retorna o mesmo valor de seno! Portanto, respostas possíveis são:
E como isso é só pra primeira volta no círculo trigonométrico, toda vez que adicionarmos () a esses ângulos, vamos “voltar” pra posição original nesse círculo, então de forma mais geral a resposta é:
Bora manter essas ideias pros próximos passos, ok?
Passo 3
Letra b)
Agora vamos escolher o contrário, seja:
Para , temos:
Pela mesma lógica da letra , vamos ter que esses dois ângulos tem o mesmo valor de seno! Então:
Letra c)
Pra começar, veja o seguinte, o ângulo é maior que ! Em graus, temos . O equivalente a ele então dentro da primeira volta é o ângulo :
Vamos continuar então essa letra partindo de:
Pra tangente a brincadeira é um pouco diferente. Afinal como:
Pra tangente de ângulos diferentes serem iguais, os ângulos devem ser:
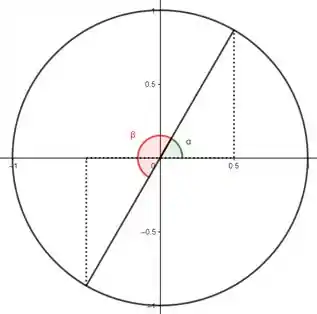
Veja que desse jeito, ou o seno e o cosseno são negativos, ou os dois são positivos. Ao dividirmos, teremos tangente positiva. Sendo , vamos ter
Para , temos:
E portanto pra termos a equação abaixo satisfeita:
Devemos ter:
Note que pra , achamos o original, então usar o ângulo equivalente da primeira volta faz sentido, né não?
Passo 4
Letra d)
Última letra e a gente fecha, beleza? Olhando bem pro círculo trigonométrico, vemos que:
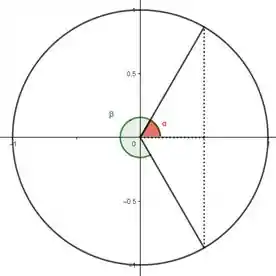
Sendo, nesse caso:
Temos:
Galera, como nosso enunciado é:
Escolhendo , vamos ter que:
A equação abaixo:
Vai ser então satisfeita com: