Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.4 - Ex. 2

Verifique suas respostas para o Exercício 1 com um recurso gráfico computacional, determinando se os gráficos de f e g são reflexões um do outro em relação à reta y = x

Passo 1

Fala galera! A questão 1 ta pedindo pra gente confirmar se g x é ou não inversa de f x nesses casos aqui:

a )   f x = 4 x ,     g x = 1 4 x

b )   f x = 3 x + 1 ,     g x = 3 x - 1

c )   f x = x - 2 3 ,     g x = x 3 + 2

d )   f x = x 4 ,     g x = x 4

Graficamente falando, isso só será verdade se g x for uma imagem espelhada de f x em relação a reta y = x ! Portanto, bora plotar os gráficos de f , g pra confirmar, belê?

Passo 2

Letra a:

f x = 4 x

g x = 1 4 x

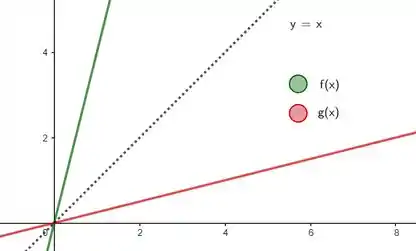
Pelo gráfico, confirmamos que g é espelho de f em relação a reta pontilhada, então de fato g é a inversa de f !

Passo 3

Letra b:

f x = 3 x + 1

g x = 3 x - 1

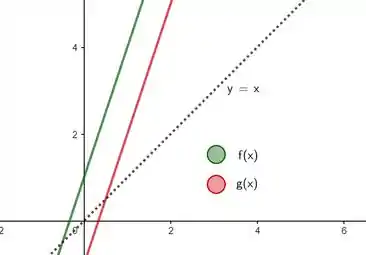
Pelo gráfico, vemos que g não é espelho de f em relação a reta pontilhada, então de fato g não é a inversa de f !

Passo 4

Letra c:

f x = x - 2 3

g x = x 3 + 2

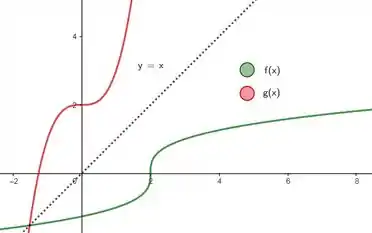
Pelo gráfico, confirmamos que g é espelho de f em relação a reta pontilhada, então de fato g é a inversa de f !

Passo 5

Letra d:

f x = x 4    

g x = x 4

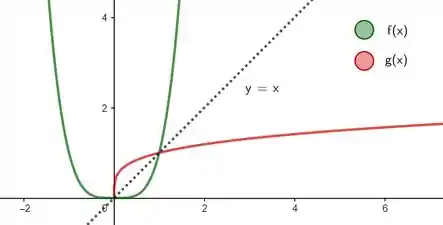
Pelo gráfico, vemos que g não é espelho de f em relação a reta pontilhada, então de fato g não é a inversa de f ! Mas meio que quase é! Note que se adicionássemos uma função

h x = - x 4

Teríamos o conjunto g , h sendo juntos a imagem espelhada de f :

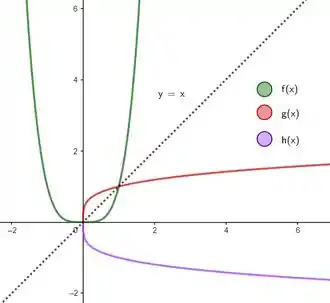
Ou seja, g x não é mesmo inversa de f x já que precisa de um “auxiliar” pra virar imagem espelhada!

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dado que x = c o s - 1 ( 1 3 ) , ache o valor exato de cada uma das funções:8. a) s e n( x )
Dado que x = c o s - 1 ( 1 3 ) , ache o valor exato de cada uma das funções:8. c) c o t g( x )
Nos Exercícios de 1 a 6, determine o valor funcional exato.6. d) s e c - 1 ( - 1 )
Dado que x = s e n - 1 ( 1 3 ) , ache o valor exato de cada uma das funções:7. a) c o s( x )
Dado que x = s e n - 1 ( 1 3 ) , ache o valor exato de cada uma das funções:7. b) t g( x )