Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 2.7 - Ex. 7
Em cada um dos problemas de 5 a 10, desenhe um campo de direções para a equação dada e diga se as soluções estão convergindo ou divergindo.
Passo 1
Para resolvermos esse problema, vamos usar um software para gerar nossos campos de direções, como sugerido pelo próprio livro, e analisar e discutir para qual valor tende as soluções da própria equação.
Passo 2
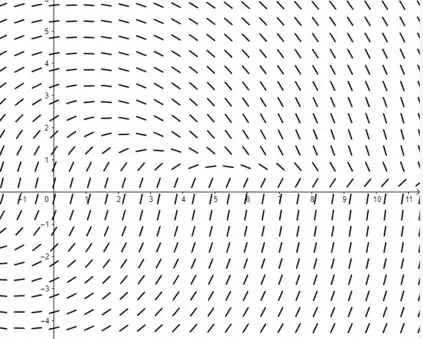
Vemos pelo esquema que as soluções estão convergindo para um único valor próximo a 1. Tanto os valores positivos quanto negativos da função estão bem comportados, de acordo com o resultado gerado pelo nosso querido GeoGebra (valeu, GeoGebra
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
15 . Suponha que determinada população satisfaz o problema de valor inicialdy/dt = r(t)y – k, y(0) = y0,em que a taxa de crescimento r(t) é dada por r(t) = (1 + sen t)/5, e k representa a taxa predató
16. A lei do resfriamento de Newton diz que a temperatura de um objeto varia a uma razãoproporcional à diferença entre sua temperatura e a temperatura ambiente. Suponha que atemperatura de uma xícara
14. Suponha que determinada população tem uma taxa de crescimento que varia com o tempo e queessa população satisfaz a equação diferencialdy/dt =(0,5 + sen t)y/5.(a) Se y(0) = 1, encontre (ou estime)
17. O calor transferido de um corpo para seu ambiente por radiação, baseado na lei de StefanBoltzmann,5 é descrito pela equação diferencial d u d t = - α u 4 - T 4 em que u(t) é a temperatura absoluta
15 . Suponha que determinada população satisfaz o problema de valor inicialdy/dt = r(t)y – k, y(0) = y0,em que a taxa de crescimento r(t) é dada por r(t) = (1 + sen t)/5, e k representa a taxa predató