Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 2.3 - Ex. 15-c
15 . Suponha que determinada população satisfaz o problema de valor inicial
dy/dt = r(t)y – k,
y(0) = y0,
em que a taxa de crescimento r(t) é dada por r(t) = (1 + sen t)/5, e k representa a taxa predatória.(a) Suponha que k = 1/5. Faça gráficos de y em função de t para diversos valores de y0 entre ½e 1.(b) Estime a população inicial crítica yc abaixo da qual a população será extinta.(c) Escolha outros valores de k e encontre a população crítica yc correspondente para cada umdeles.(d) Use os dados encontrados nos itens (b) e (c) para fazer o gráfico de yc em função de k.
Passo 1
No passo a) descobrimos coisas importantes. Que nossa função não tem uma solução analitica é uma bem importante. Podemos observar abaixo
Podemos deixar ela um pouco mais palatavel como
Como não podemos resolver essa integral podemos expressar ela por uma expansão em Taylor como podemos observar abaixo
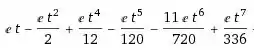
Uma coisa importante é que em a) tinhamos que , como queremos variar k logo podemos substituir isso na nossa euqação e obter
Passo 2
Queremos saber o valor de que seja tao pequeno que não de tempo da população se recuperar e crescer. O gráfico de uma função de y pode ser observada abaixo
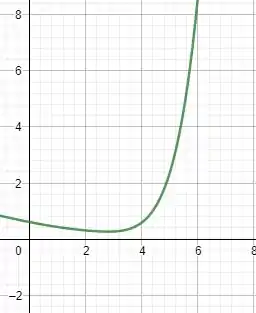
A função decresce antes de subir, se o valor inicial for muito baixo. A população se extinguira.
Passo 3
Então queremos
Por propriedades matematica ou
Ou
E como a função exponencial nunca se anula, entao temos que
E infelizmente, como não temos resolver essa integral somos obrigados a parar por aqui.
Terminamos por aqui. Te vejo na próxima resolução
: )