Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 2.4 - Ex. 19
Em cada um dos problemas de 17 a 20, desenhe um campo de direções e desenhe (ou esboce) gráficos de diversas soluções da equação diferencial dada. Descreva como as soluções parecem se comportar quando t aumenta e como seus comportamentos dependem do valor inicial quando t = 0.
Passo 1
Vamos lá!!!
A primeira coisa é esboçar o gráfico em campo de direções, para a função abaixo:
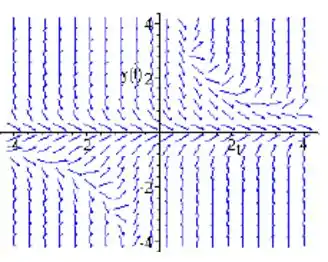
Passo 2
Ao analisarmos a equação, podemos concluir algumas coisas:
Vamos lá!!!
1ª) Quando y tender para valores cada vez mais positivo e maiores, o valor de terá que ser necessariamente maior que nove.
2ª) Agora quando y for tender a zero, necessariamente o valor inicial de y () terá que ser menor ou igual a nove.
Resposta
Exercícios de Livros Relacionados
Em cada um dos problemas de 3 a 6, seja ϕ 0 t = 0 e defina ϕ n t é pelo método das aproximações sucessivas.Determine ϕ n ( t ) para um valor arbitrário de n Faça o gráfico de ϕ n t = ϕ t para n = 1 ,
Em cada um dos problemas de 3 a 6, seja ϕ 0 t = 0 e defina ϕ n t é pelo método das aproximações sucessivas.Determine ϕ n ( t ) para um valor arbitrário de n Faça o gráfico de ϕ n t = ϕ t para n = 1 ,
Seja ϕ n x = x n para 0 ≤ x ≤ 1 e mostre que lim n → ∞ ϕ n x = 0 ,0 ≤ x1 1 , x = 1 Esse exemplo mostra que uma sequência de funções contínuas pode convergir a uma função limite que é descontínua.
Em cada um dos Problemas 11 e 12, seja ϕ 0 t = 0 e use o método das aproximações sucessivas para aproximar a solução do problema de valor inicial dado.Calcule ϕ 1 t , … ,ϕ 4 t ou (se necessário) aprox
Nos problemas de 15 a 18, indicamos como provar que a sequência ϕ n t , definida pelas equações de (4) a (7), converge.Se ϕ n - 1 t e ϕ n t são elementos da sequência ϕ n t , use o resultado do proble