Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 9.3 - Ex. 12

Em cada um dos problemas de 5 a 18:

(a) Determine todos os pontos críticos do sistema de equações dado.

(b) Encontre o sistema linear correspondente perto de cada ponto crítico.

(c) Encontre os autovalores de cada sistema linear. O que você pode concluir sobre o sistema não linear?

(d) Desenhe um retrato de fase do sistema não linear para confirmar suas conclusões, ou para estendê-las nos casos em que o sistema linear não fornece informações definidas sobre o sistema não linear.

12. d x / d t = 1 + x sin ⁡ y ,         d y / d t = 1 - x - cos ⁡ y

Passo 1

L e t r a   A :

Primeiro devemos encontrar os pontos crítico desse sistema de EDO:

d x d t = 1 + x sin ⁡ y ,       d y d t = 1 - x - cos ⁡ y       →

Ponto crítico acontece quando a derivada é 0 , ou seja:

0 = 1 + x sin ⁡ y ,       0 = 1 - x - cos ⁡ y

Um ponto que a gente já consegue ver que é ponto crítico é o x = 0 e y = 0 :

x = 0         e           y = 0  

Mas esse não é o único ponto crítico! Se você jogar esse sistema no WolframAlpha (já que podemos utilizar o computador nessa tarefa) e apertar Enter (batsta copiar 0 = 2 x + y + x y 3 ,         0 = x - 2 y - x y

do jeito que está aí no WolframAlpha). Ele vai ter também como resultado, os pontos:

0 ,   2 π n         e           2 ,   2 π n + π         o n d e             n   é   i n t e i r o

Ou seja, qualquer valor que y assuma desde que x = 0 ou x = 2 e y = 2 π n , onde n é um inteiro, é também ponto crítico, saca? Veja que o nosso ponto x = 0 e y = 0 encontrado, também faz parte desse conjunto, pasta tomar n = 0 :

0 ,   0 ∈ 0 ,   2 π n   |       n ∈ Z

Resumindo: temos dois conjuntos de pontos críticos:

0 ,   2 π n           e             2 ,   2 π n + π

Passo 2

L e t r a   B :  

A primeira coisa para determinar um sistema linear próximo a um ponto crítico é pegar a o sistema que estamos trabalhando:

d x d t = 1 + x sin ⁡ y ,       d y d t = 1 - x - cos ⁡ y →

E chamar...

F x ,   y = 1 + x sin ⁡ y         e                 G x ,   y = 1 - x - cos ⁡ y    

Agora, dessas duas funções aí, F e G , devemos extrair a matriz Jacobiana dada por:

J x ,   y = F x F y G x G y

Calculando essas derivadas parciais então...

J x ,   y = sin ⁡ y 1 + x cos ⁡ y - 1 sin ⁡ y

Beleza! Agora temos que substituir os nossos pontos críticos. Como são dois, vou fazer isso em dois passos extras, ok?

Passo 3

Primero o do ponto 0 ,   0 , isto é:

J x ,   y = sin ⁡ y 1 + x cos ⁡ y - 1 sin ⁡ y   →

J 0 ,   2 π n = sin ⁡ y 1 + x cos ⁡ y - 1 sin ⁡ y   →

J 0 ,   2 π n = sin ⁡ 2 π n cos ⁡ 2 π n - 1 sin ⁡ 2 π n   →

Como o seno de qualquer número que múltiplo de 2 π é 0 e o cosseno é 1 ...

J 0 ,   2 π n = 0 1 - 1 0

De acordo com a teoria, o sistema de EDO linear que aproxima a não linear nesse caso é:

x ' y ' = 0 1 - 1 0 x - 0 y - 2 π n

Lembre-se que n é um valor inteiro qualquer, assim teremos infinitos sistemas como esse!

x ' é o d x / d t e y ' o d y / d t .

Passo 4

Agora vamos fazer o mesmo para os pontos   2 ,   2 π n + π :

J x ,   y = sin ⁡ y 1 + x cos ⁡ y - 1 sin ⁡ y

J 2 ,   2 π n + π = sin ⁡ 2 π n + π 3 cos ⁡ 2 π n + π - 1 sin ⁡ 2 π n + π

Nesse caso, o seno continua sendo 0 paraqualquer n enquanto o cosseno, vira - 1 :

J 2 ,   2 π n + π = 0 - 1 - 1 0

Então, o sistema linear de aproximação nesse caso é:

x ' y ' = 0 - 1 - 1 0 x + 2 y + 2 π n + π

Passo 5

L e t r a   C :

Novamente, como temos dois pontos, teremos aqui que separar o cálculo para esses dois casos. Vamos começar descobrindo os autovalores associados a matriz do primeiro ponto crítico que achamos:

A = 0 1 - 1 0       →

det ⁡ A - λ I = det ⁡ - λ 1 - 1 - λ =

Aqui é tranquilo, podemos encontrar esses valores de λ na mão resolvendo esse determinante:

λ 2 + 1 = 0       →

λ = ± - 1

λ = ± i

Observando a tabela 9.3.1 do nosso querido Boyce, concluímos que o sistema não linear, pelo menos próximo a ao ponto crítico é indeterminado já que a solução foi um número complexo puro!

Passo 6

Para o segundo caso, onde temos essa matriz de coeficientes aqui:

A = 0 - 1 - 1 0

Podemos...

det ⁡ A - λ I = det ⁡ - λ - 1 - 1 - λ =

λ 2 - 1 = 0     →

λ = ± 1

λ 1 = 1         e           λ 2 = - 1

Ao redor de qualquer ponto do tipo 2 ,   2 π n + π teremos, pela consulta a tabela, um sistema instável!

Passo 7

L e t r a   D :

Nesse caso, para desenhar o retrato de fase da nossa EDO, também usaremos o WolframAlpha simplesmente copiando a equação

d x / d t = 2 x + y + x y 3 ,         d y / d t = x - 2 y - x y

E apertando Enter. Gerando esse retrato de fase aqui:

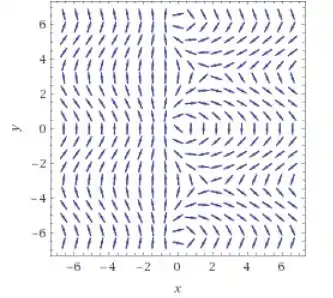
Repare nas instabilidades em x = 2 e já bem próximo do x = 0 existe alguns pontos de estabilidades que não conseguimos identificar!

Resposta

Letra A: 0 ,   2 π n           e             2 ,   2 π n + π

Letra B:

x ' y ' = 0 1 - 1 0 x y + 2 π n                   e                   x ' y ' = 0 - 1 - 1 0 x + 2 y + 2 π n + π

Letra C:

λ = ± i             e               λ 1 = 1   ,   λ 2 = - 1

Letra D:

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em cada um dos problemas de 1 a 4, verifique se (0, 0) é um ponto crítico, mostre que o sistema é localmente linear e discuta o tipo e a estabilidade do ponto crítico (0, 0) examinando o sistema linea
Em cada um dos problemas de 1 a 4, verifique se (0, 0) é um ponto crítico, mostre que o sistema é localmente linear e discuta o tipo e a estabilidade do ponto crítico (0, 0) examinando o sistema linea
Em cada um dos problemas de 5 a 18:(a) Determine todos os pontos críticos do sistema de equações dado.(b) Encontre o sistema linear correspondente perto de cada ponto crítico.(c) Encontre os autovalor
Em cada um dos problemas de 5 a 18:(a) Determine todos os pontos críticos do sistema de equações dado.(b) Encontre o sistema linear correspondente perto de cada ponto crítico.(c) Encontre os autovalor
Em cada um dos problemas de 1 a 4, verifique se (0, 0) é um ponto crítico, mostre que o sistema é localmente linear e discuta o tipo e a estabilidade do ponto crítico (0, 0) examinando o sistema linea