Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 8.1 - Ex. 11

Em cada um dos problemas de7 a 12,encontre valores aproximados da solução do problema de valor inicial dado em t   =   0,5 ; 1,0 ; 1,5   e   2,0 .

(a) Useo método de Euler com h   =   0,025 .  

(b) Useo método de Euler com h   =   0,0125 .

(c) Useo método de Euler inverso com h   =   0,025 .

(d) Useo método de Euler inverso com h   =   0,0125 .

11. y ' = 4 - t y 1 + y 2 ,           y 0 = - 2

Passo 1

Bora lá pro nosso probleminha!

a) Olha só! A fórmula de E u l e r   tem a seguinte cara:

y n + 1 = y n + h 4 - t n y n 1 + y n 2

Só que...

t n = t 0 + n h

É claro, pra facilitar a nossa vida, temos que...

t 0 = 0

O que nos leva à...

y n + 1 = y n + 4 h - n h 2 y n 1 + y n 2

Onde sabemos que...

y 0 = - 2

Desse modo, vamos como pede o problema, utilizar um método computacional simples... Um códigozinho simples em C , C + + ou P y t h o n resolveria isso.

Basta usar a seguinte estrututa para o código...

P a s s o   1 : D e f i n i r   a   f u n ç ã o   y n + 1

P a s s o   2 : D e f i n i r   o   t a m a n h o   d o   p a s s o   h   e   o   n ú m e r o   d e   p a s s o s   n

P a s s o   3 : P a r a   i   d e   1   a t é   u m   t a m a n h o   d e 2 h   f a ç a

P a s s o   4 :

y n + 1 = y n + 4 h - n h 2 y n 1 + y n 2

i = i + 1

n = n + 1

P a s s o   5 : E s c r e v a l   y n + 1

P a s s o   6 : F i m

É importante trabalhar com y n + 1 e y n na forma de vetor! Facilita muito a nossa vida!

Bom! Usando o seguinte código confeccionado em C ...

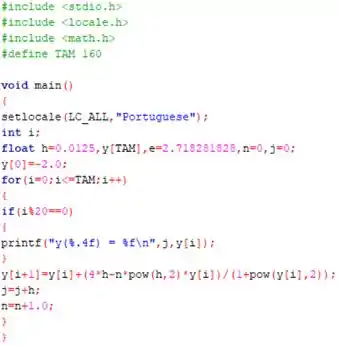
Chegamos até o seguinte resultado...

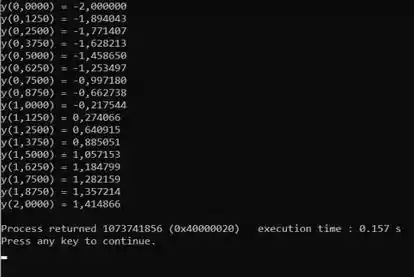
E obtemos a tabela abaixo, pros valores que procurávamos...

Passo 2

b) Para resolver essa letra, basta substituir uma coisa pequeninha no código do P a s s o   2 . Só precisa trocar o h   por 0,0125 .

E dessa vez o tamanho de iterações de n vai ser dado por:

T A M = 2 0,0125 = 160

Compilando o código, obtemos que...

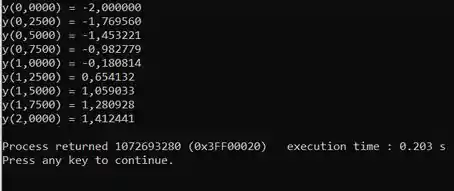
De modo que chegamos até a seguinte tabela...

Passo 3

c) Para fazer o método de Euler inverso, temos que pegar a seguinte relação abaixo...

y n + 1 = y n + h 4 - t n + 1 y n + 1 1 + y n + 1 2

E como sabemos da condição inicial...

t 0 = 0

E também que no método inverso, devemos fazer...

t n + 1 = n + 1 h

Nossa relação vai ficar assim...

y n + 1 ⋅ 1 + y n + 1 2 = y n ⋅ 1 + y n + 1 2 + 4 h - ( n + 1 ) h 2 y n + 1

Onde sabendo do valor de y em 0 ...

y 0 = 1

Ao fazer nossas iterações, com h = 0,025 , até chegar em t = 2 , obtemos a seguinte tabela, considerando os valores pedidos pelo enunciado...

Passo 4

d) Para finalizar, uma vez que já sabemos da fórmula...

y n + 1 ⋅ 1 + y n + 1 2 = y n ⋅ 1 + y n + 1 2 + 4 h - ( n + 1 ) h 2 y n + 1

Onde sabendo do valor de y em 0 ...

y 0 = 1

Ao fazer nossas iterações, com h = 0,0125 , até chegar em t = 2 , obtemos a seguinte tabela, considerando os valores pedidos pelo enunciado...

Resposta

a)

b)

c)

d)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

22. Considere oproblema de valor inicialy ' =c o s5 π t , y 0 = 1 (a) Determine a solução y=ϕ ( t ) e desenhe o gráfico dey=ϕ ( t ) para 0 ≤t≤1 . (b) Determine valores aproximados para ϕ ( t ) em t=0,
Em cada um dos problemas de 7 a 12, encontre valores aproximados da solução do problema de valorinicial dado em t = 0,5; 1,0; 1,5 e 2,0.(a) Use o método de Euler com h = 0,025.(b) Use o método de Eule
Em cada um dos problemas de 1 a 6, encontre valores aproximados da solução do problema de valorinicial dado em t = 0,1; 0,2; 0,3 e 0,4.(a) Use o método de Euler com h = 0,05.(b) Use o método de Euler
Em cada um dos problemas de 1 a 6, encontre valores aproximados da solução do problema de valorinicial dado em t = 0,1; 0,2; 0,3 e 0,4.(a) Use o método de Euler com h = 0,05.(b) Use o método de Euler
Em cada um dos problemas de 1 a 6, encontre valores aproximados da solução do problema de valorinicial dado em t = 0,1; 0,2; 0,3 e 0,4.(a) Use o método de Euler com h = 0,05.(b) Use o método de Euler