22. Considere oproblema de valor inicial
(a) Determine a solução e desenhe o gráfico de para .
(b) Determine valores aproximados para em e usando o método de Euler com . Desenhe um gráfico com segmentos de reta para a solução aproximada e compare o com o gráfico da solução exata.
(c) Repita o cálculo do item para , mas com .
(d) Mostre que por meio de cálculo do erro de truncamento local, que nenhum desses tamanhos de passo é suficientemente pequeno. Determine um valor de que garanta que o erro de truncamento local é menor do que ao longo do intervalo . O fato de ser necessário um valor tão pequeno de é consequência de o ser tão grande.
Passo 1
a) Olha só! Para obter a solução dado que temos a equação de primeira ordem basta integrar essa sabendo que .
Ou seja, vamos ter que somar ao resultado da integral de ...
De modo que o nosso gráfico para essa função, utilizando um software qualquer desses de plotar gráfico, , , ou , fica assim...
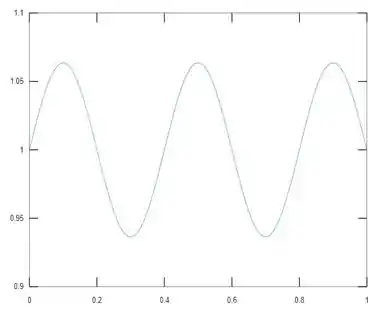
Passo 2
b) A fórmula de para a equação diferencial desse nosso probleminha tem a seguinte cara...
Só que...
Onde temos que...
O que nos leva à...
De modo que para resolver essa letra, vamos seguir aquele velho algoritmo que a gente vinha fazendo anteriormente...
Assim, realizando um total de iterações igual a...
No seguinte código abaixo...
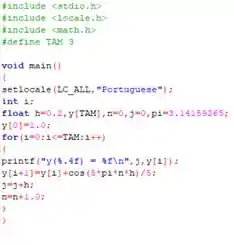
Obtemos nossa resposta, igual à...
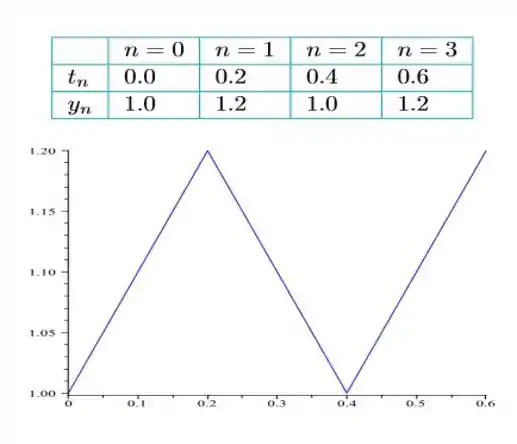
Passo 3
c) Para este item, vamos pegar o mesmo código da letra anterior. Só que vai mudar o número de iterações e o tamanho do passo ...
Como e ... O número de iterações vai ser dado por...
Desse modo, a nossa resposta vai ser igual a...
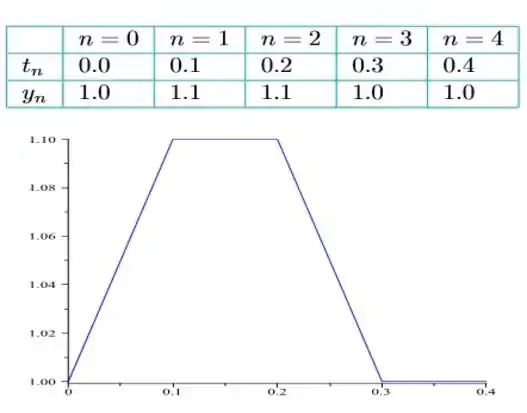
Passo 4
d) Pra finalizar, vamos verificar se o tamanho do passo é pequeno mesmo, utilizando o erro de truncamento...
Nós sabemos que:
Derivando uma vez, ficamos com...
Derivando outra vez, obtemos que...
Utilizando a fórmula para obter o erro de truncamento local...
Não podendo esquecer do intervalo de ...
Chegamos até a seguinte relação...
O que nos fornece...
Logo, vimos que um tamanho de passo decente teria que ser menor do que ...
Resposta
a)
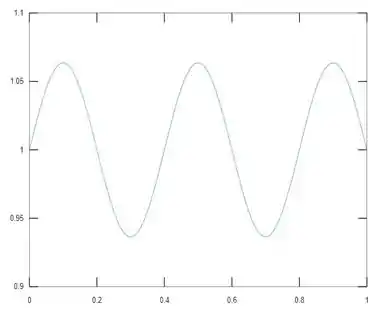
b)
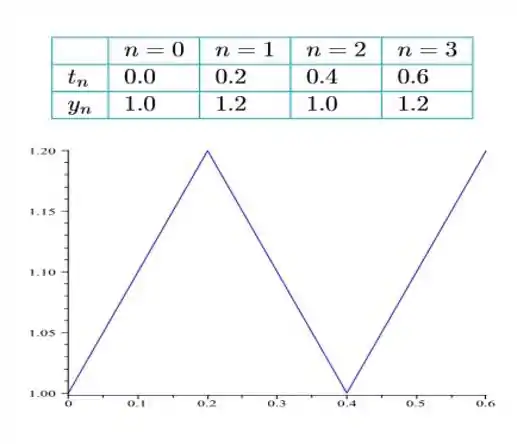
c)
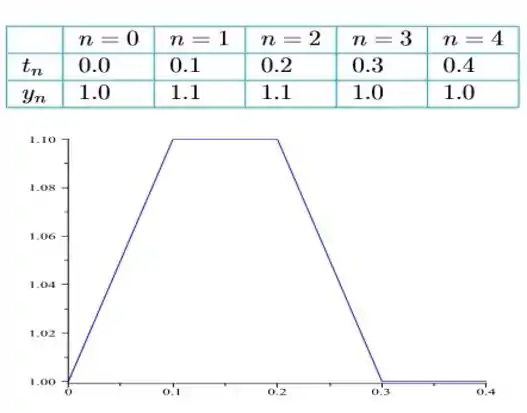
d)