Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 8.4 - Ex. 2
Em cada um dos problemas de 1 a 6, determine um valor aproximado da solução em t = 0,4 e t = 0,5 usando o método especificado. Para os valores iniciais, use o método de Runge-Kutta; veja os Problemas de 1 a 6 da Seção 8.3. Compare os resultados dos vários métodos entre si e com a solução exata (se disponível).
(a) Use o método de previsão ecorreção de quarta ordem comh=0,1. Use a fórmula de correção uma vez em cada passo.
(b) Use o método de Adam-Moulton de quarta ordem com h = 0,1.
(c) Use o método inverso de diferenciação de quarta ordem com h = 0,1.
1.
Passo 1
a) Vamos começar usando a notação .
Desse modo, a fórmula do método preditor vai ficar assim...
Já no caso da fórmula de correção com ... Temos que:
Usando os valores iniciais gerados pelo método de . No caso peguemos os valores da figura abaixo do código que fizemos na para essa mesma com passo ;
Ou seja, pegando a seguinte tabela abaixo...
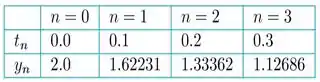
Para o método preditor com ...
Sendo que...
Obtemos que...
Passo 2
No caso do método corretor, temos que para ...
Com...
Chegamos ao seguinte resultado:
Seguindo o mesmo procedimento para outros , com .... Chegamos até a seguinte tabela abaixo...
Passo 3
b) Presta atenção! O método de Adam-Moulton tem a seguinte cara abaixo...
Com , temos que...
Até aí tá bem parecido com o método corretor. O diferencial é que...
Uma vez que a é linear, nós vamos fazer...
E com isso, para ... Sabendo dos valores abaixo...
Alcançamos o resultado para :
Seguindo o mesmo procedimento para ...Obtemos a seguinte tabela abaixo
Passo 4
c) No caso do método inverso de diferenciação de quarta ordem com ... Bora fazer;
Só que neste método, o diferencial assim como no método anterior, é que...
O que nos faz ficar com...
E como já sabemos todos os valores de cada variável aí, fazendo as iterações, para e ... Obtemos a tabela abaixo:
Resposta
a)
b)
c)
