Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 11.2 - Ex. 8
Em cada um dos problemas de 6 a 9, encontre os coeficientes da expansão em autofunções da função dada, usando as autofunções normalizadas do Problema 1.
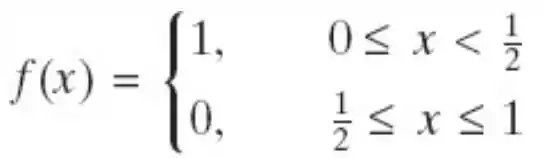
Passo 1
Escrevendo aqui a autofunção encontrada no problema 1 nós teremos:
Para , com isso nossa integral para o termo nós teremos:
Já que é uma função composta então teremos duas integrais, portanto o termo fica:
Substituindo para que tenhamos uma função em termos de :
Interpretando o cosseno, nós iremos ter valores de cosseno iguais a
O que nos dá valores de cosseno iguais a
Resposta
Exercícios de Livros Relacionados
Considere a equação de Legendre (veja os problemas de 22 a 24 da Seção 5.3)sujeita às condições de contornoOs autovalores para esse problema são λ1 = 2, λ2 = 4 · 3, . . ., λn = 2n(2n – 1), . . . e as
Considere a equação de Legendre (veja os problemas de 22 a 24 da Seção 5.3)sujeita às condições de contornoOs autovalores para esse problema são λ1 = 2, λ2 = 4 · 3, . . ., λn = 2n(2n – 1), . . . e as
Considere o problema de valores de contorno.Mostre que, se m, n = 0, 1, 2, . . . , então
Considere o problema de valores de contorno.Encontre uma solução formal para o problema não homogêneoem que f é uma função dada, contínua em 0 ≤ x ≤ 1, e μ não é um autovalor do sistema homogêneo asso
Este problema desenvolve outros resultados associados à convergência na média. Sejam Rn(a1, . . . , an), Sn(x) e ai definidos pelas Eqs. (6), (2) e (9), respectivamente. Mostre que