Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 11.1 - Ex. 21

Considere o problema

y ' ' + λ y = 0 ,     2 y 0 + y ' 0 = 0 ,     y 1 = 0

( a ) Encontre a equação satisfeita pelos autovalores positivos.

( b ) Mostre que existe uma sequência infinita de tais autovalores.

( c ) Encontre   λ 1 e λ 2 . Depois mostre que λ n   ≅   2 n   +   1 π 2 2 para n grande

( d ) Encontre a equação satisfeita pelos autovalores negativos

( e ) Mostre que existe exatamente um autovalor negativo e encontre seu valor.

Passo 1

A solução para essa equação diferencial será:

y = c 1 s e n λ x + c 2 cos ⁡ λ x

y ' = c 1 λ c o s λ x - c 2 λ s e n ( λ x )

Aplicando as condições de contorno nós teremos:

2 0 + c 2 + c 1 λ + 0 = 0

2 c 2 + c 1 λ = 0

E

y 1 = c 1 s e n λ + c 2 cos ⁡ λ = 0

Como a segunda equação não nos dá algo muito palpável então vamos para a primeira, se tivermos c 2 = 1 e c 1 = - 2 λ , então podemos ter uma equação possível igual a:

y = - 2 λ s e n λ x + cos ⁡ λ x

Ou seja para y ( 1 ) teremos:

y 1 = - 2 s e n λ + λ cos ⁡ λ = 0

Passo 2

Pela expressão de y ( 1 ) podemos ver que:

- 2 s e n λ + λ cos ⁡ λ = 0

λ = 2 s e n λ cos ⁡ λ = 2 tan ⁡ λ

E se plotarmos os gráficos de y 1 = λ e de y 2 = 2 tan ⁡ λ , encontraremos:

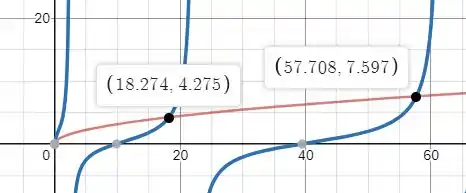
Se fizermos para o caso em λ = 0 nós encontraremos que esse autovalor não é válido. Portanto pelo gráfico vemos que os dois primeiros autovalores válidos são somente λ 1 = 18.274 e λ 2 = 57.708 .

Passo 3

No exemplo 1 dessa seção se comenta que se tivermos autovalores negativos a solução dessa equação será igual a:

y = c 1 s e n h u x + c 2 cosh ⁡ u x

y ' = c 1 u cosh ⁡ u x + c 2 u s e n h ( u x )

Colinha de funções hiperbólicas:

s e n h x = e x - e - x 2 ; cosh ⁡ x = e x + e - x 2

s e n h 0 = 0 ;   cosh ⁡ 0 = 1

d d x s e n h x = cosh ⁡ x ;   d d x cosh ⁡ x = s e n h ( x )

Onde u = - λ , então aplicando as condições de contorno nós teremos:

2 y 0 + y ' 0 = 0

2 c 1 s e n h 0 + 2 c 2 cosh ⁡ 0 + c 1 u c o s h 0 + c 2 u s e n h 0

2 c 2 + c 1 u = 0

O que não é diferente do caso para autovalores positivos, somente o fato de que agora as funções são hiperbólicas e que adotaremos u invés de λ , logo para y ( 1 ) teremos a seguinte equação:

,     y 1 = 0

y ( 1 ) = - 2 s e n h u + u cos h ⁡ u = 0

Passo 4

Para encontrar o autovalor negativo nós ver que a equação de y ( 1 ) pode ser vista como:

- 2 s e n h u + u cos h ⁡ u = 0

u = 2 s e n h u cosh ⁡ u = 2 tanh ⁡ u

E plotando os gráficos de y 1 = u e y 2 = 2 t a n h ⁡ ( u ) vemos que eles se interceptam em somente um ponto e que será:

u = 3.667

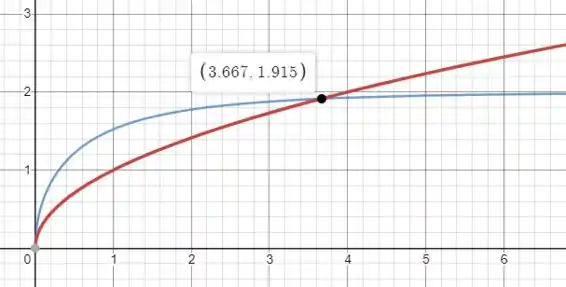
Mas como queremos o autovalor λ   e u = - λ , então λ = - 3.667

Resposta

a )   y 1 = - 2 s e n λ + λ cos ⁡ λ = 0

b )   2 c 2 + c 1 λ = 0 → i n u m e r o s   s o l u ç õ e s   p o d e m   s e r   e s c r i t a s   p a r a   c 1   e   c 2

c )   λ 1 = 18.274 e λ 2 = 57.708 .

d )   y 1 = - 2 s e n h u + u cos h ⁡ u = 0 , u = - λ

e )   λ = - 3.667

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em cada um dos problemas de 1 a 14, encontre a solução geral da equação diferencial dada. y ' ' + y ' = 3 sen ⁡ 2 t + t cos ⁡ 2 t
Considere a equação y ' ' - 3 y ' + 4 y = 2 e - t Lembre-se de que y 1 t = e - t e y 2 t = e 4 t são soluções da equação homogênea associada. Adaptando o método de redução de ordem (Seção 3.4), busque
Nesse problema, vamos esboçar uma demonstração de que os autovalores do problema de valores de contorno (18), (19) são reais. exp ⁡ i μ π - exp ⁡ - i μ π = 0 (a) Escreva a solução da Eq. (18) como y=k
Em cada um dos problemas de 1 a 13, resolva o problema de valores de contorno dado ou mostre que não tem solução: x 2 y ″ + 3 x y ' + y = x 2,y ( 1 )=0 ,y ( e )=0
Em cada um dos problemas de 1 a 13, resolva o problema de valores de contorno dado ou mostre que não tem solução: x 2 y ″ + 5 x y ' + 4 + π 2 y = ln ⁡ x ,y 1 = 0 ,y ( e ) = 0