Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 11.4 - Ex. 4a
Considere a equação de Legendre (veja os problemas de 22 a 24 da Seção 5.3)
sujeita às condições de contorno
Os autovalores para esse problema são λ1 = 2, λ2 = 4 · 3, . . ., λn = 2n(2n – 1), . . . e as autofunções associadas são os polinômios de Legendre de grau ímpar.
Mostre que
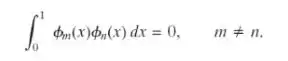
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para analisarmos as deformações verticais de uma barra em suas condições de contorno. Parece muita coisa, mas é tranquilo. Partiu??
Passo 2
Ok, nosso primeiro passo vai ser analisar a equação dada.
Para
Passo 3
Pronto!! Agora é só fazermos umas matemágicas aí pra achar o resultado!!
Resposta
Exercícios de Livros Relacionados
Um rastreador não reativo em uma concentração c0 está sendo continuamente introduzido em um fluxo regular na extremidade rio acima de uma coluna de comprimento L cheia de um meio granular homogêneo. S
Considere o problema de Sturm-Liouvilleem que p, q e r satisfazem as condições enunciadas no texto.Mostre que, se q(x) ≥ 0 e, se β1/β2 e – α1/α2 não forem negativos, então o autovalor λ será maior do
Considere o problema de Sturm-Liouvilleem que p, q e r satisfazem as condições enunciadas no texto.Mostre que, se λ for um autovalor e se φ for uma autofunção associada, entãodesde que α2 ≠ 0 e β2 ≠ 0
Substâncias dissolvidas em um aquífero são transportadas por dois mecanismos separados. O processo pelo qual um soluto é transportado pelo grande movimento do fluxo da água subterrânea é chamado de ad
Considere o problema de Sturm-Liouvilleem que p, q e r satisfazem as condições enunciadas no texto.Mostre que, se q(x) ≥ 0 e, se β1/β2 e – α1/α2 não forem negativos, então o autovalor λ será maior do