Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 8.2 - Ex. 6

Em cada um dos problemas de 1 a 6, encontre valores aproximados da soluçãodo problema de valor inicial dado em t = 0,1; 0,2; 0,3 e 0,4. Compare osresultados comos obtidos pelométodo de Euler e pelométodo de Euler inverso na Seção 8.1 e com a solução exata (se disponível).

(a) Useo método de Euler aprimoradocom h   =   0,05 .

(b) Useo método de Euler aprimoradocom h   =   0,025 .

(c) Use o método de Euler aprimorado com h   = 0,0125 .

6. y ' = t 2 - y 2 sen ⁡ y ,     y 0 = - 1

Passo 1

Bora lá pra mais um probleminha sobre método de E u l e r aperfeiçoado.

Olha só! A fórmula aperfeiçoada de E u l e r para a equação diferencial do nosso problema será...

y n + 1 = y n + h 2 t n 2 - y n 2 sen ⁡ y n + h 2 t n + 1 2 - K n 2 sen ⁡ K n

Sendo que K n é igual à...

K n = y n + h t n 2 - y n 2 sen ⁡ y n

Na prática, o que estamos fazendo é uma iteração dentro de outra iteração. Voltando ao que interessa, não podemos esquecer que...

t n = t 0 + n h

Com t 0 = 0 ...

Desse modo, nossa expressão geral y n + 1 vai ser...

y n + 1 = y n + h 2 t n 2 - y n 2 sen ⁡ y n + h 2 t n + 1 2 - K n 2 sen ⁡ K n

y n + 1 = y n + h 2 n 2 h 2 - y n 2 sen ⁡ y n + h 2 [ n + 1 ) 2 h 2 - K n 2 sen ⁡ K n

Agora vamos dar um jeito de resolver esse problema computacionalmente.

Passo 2

Para isso, vamos usar a seguinte estrutura abaixo em forma de algoritmo...

P a s s o   1 : D e f i n i r   a   f u n ç ã o   y n + 1  

P a s s o   2 : D e f i n i r   o   t a m a n h o   d o   p a s s o   h   e   o   n ú m e r o   d e   p a s s o s   n    

P a s s o   3 : P a r a   i   d e   1   a t é   u m   t a m a n h o   d e   0.4 h   f a ç a  

P a s s o   4 :  

K n = y n + h t n 2 - y n 2 sen ⁡ y n

y n + 1 = y n + h 2 n 2 h 2 - y n 2 sen ⁡ y n + h 2 [ n + 1 ) 2 h 2 - K n 2 sen ⁡ K n  

i = i + 1  

n = n + 1  

P a s s o   5 : E s c r e v a   y n + 1

P a s s o   6 : F i m

Passo 3

a) Desse modo, utilizando uma linguagem de programação qualquer, C ou P y t h o n , é possível determinar o que a gente quer. No caso, bora usar a C ...

Usando o seguinte código abaixo...

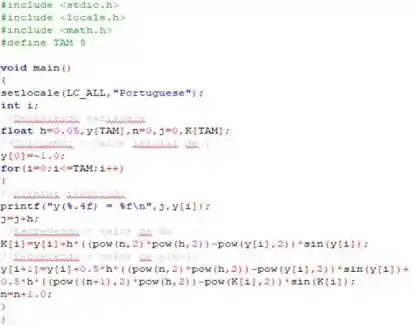
E compilando ele, num total de iterações igual à...

T A M = 0.4 h = 0.4 0.05 = 8

Obtemos os seguintes valores da tabela abaixo...

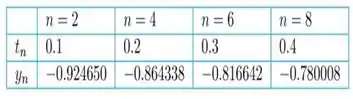
Passo 4

b) Já nessa letra, só basta alterar duas coisas no código confeccional. Primeiro, o valor de h   que vai ser igual a 0.025 .

E depois o tamanho T A M de iterações, que vai valer...

T A M = 0.4 0.025 = 16

Desse modo, compilando o código, obtemos que...

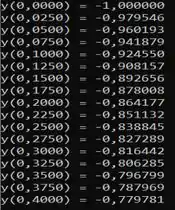
E chegamos até a seguinte tabela...

Passo 5

c) E pra finalizar... Nessa última letra, o tamanho do passo h vai ser 0.0125

De modo que precisaremos de um total de iterações igual à...

T A M = 0.4 h = 0.4 0.0125 = 32

E compilando o código, já com essas duas alterações...

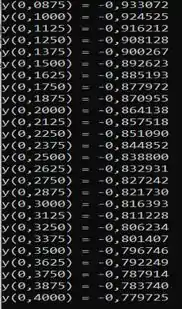
Obtemos a seguinte tabela...

Pronto! Exercício finalizado!

Resposta

a)

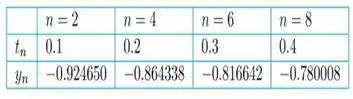
b)

c)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em cada um dos Problemas 16 e 17, use a solução exata ϕ ( t ) para determinar e n + 1 e uma cota para e n em qualquer passo no intervalo 0≤t≤1 para o método de Euler aprimorado para o problema de valo
Em cada um dos problemas de 18 a 21 , efetueum passo do método de Euler e do método de Euler aprimorado usando o tamanho de passo h=0,1 . Suponha que se deseja um erro de truncamento local não maior d
Em cada um dos problemas de 18 a 21 , efetueum passo do método de Euler e do método de Euler aprimorado usando o tamanho de passo h=0,1 . Suponha que se deseja um erro de truncamento local não maior d
22. A fórmula de Euler modificada parao problema de valor inicial y '=f ( t , y ) , y ( t 0 )=y 0 , é dada por y n + 1 = y n + h f [ t n + 1 2 h , y n + 1 2 h f ( t n , y n ) ] Seguindo o procedimento
Em cada um dos problemas de 18 a 21 , efetueum passo do método de Euler e do método de Euler aprimorado usando o tamanho de passo h=0,1 . Suponha que se deseja um erro de truncamento local não maior d