Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 7.6 - Ex. 5

Em cada um dos problemas de 1 a 6 :

( a ) Expresse a solução geral do sistema de equações dado como combinação e de funções reais

( b ) Desenhe, também um campo de direções, esboce algumas trajetórias e descreva o comportamento das soluções quando t → ∞

x ' = 1 - 1 5 - 3 x

Passo 1

Resolvendo os autovalores dessa matriz nós teremos:

d e t 1 - r - 1 5 - 3 - r = 0

1 - r - 3 - r + 5 = 0

r 2 + 3 - 1 r - 3 + 5 = 0

r 2 + 2 r + 2 = 0

Resolvendo essa equação do segundo grau nós teremos:

r 1 ; r 2 = - 2 2 ± 1 2 4 - 4 × 2 = - 1 ± 2 i 2 = - 1 ± i

E esses são os autovalores desse sistema

Passo 2

Utilizando r = - 1 - i nós teremos o seguinte autovetor:

1 + 1 + i - 1 5 - 3 + 1 + i ξ 1 1 ξ 2 1 = 0

2 + i - 1 5 - 2 + i ξ 1 1 ξ 2 1 = 0

Um vetor que podemos pegar é na primeira linha que será:

2 + i ξ 1 1 - ξ 2 1 = 0

Onde podemos escrever ξ 1 1 e ξ 2 1 como:

ξ 1 = ξ 1 1 ξ 2 1 = 1 2 + i

Esse resultado satisfaria a segunda linha também ( mesmo que o auto vetor na segunda linha possa ter uma cara diferente, na verdade é a mesma coisa).

Então a solução será:

x 1 = 1 2 + i e - 1 + i t = 1 2 + i e - t - i t = 1 2 + i e - t   e - i t

x 1 = 1 2 + i e - t   cos ⁡ - t + i   s e n - t

x 1 = 1 2 + i e - t ( cos ⁡ t - i   s e n   t )

Separando a parte real da parte imaginária nós teremos:

x 1 = cos ⁡ t 2 cos ⁡ t + s e n   t e - t + i - s e n   t - 2   s e n   t + cos ⁡ t e - t

E portanto a solução geral será:

x = c 1 cos ⁡ t 2 cos ⁡ t + s e n   t e - t + c 2 - s e n   t - 2   s e n   t + cos ⁡ t e - t

Passo 3

Plotando o campo de direções desse sistema nós teremos:

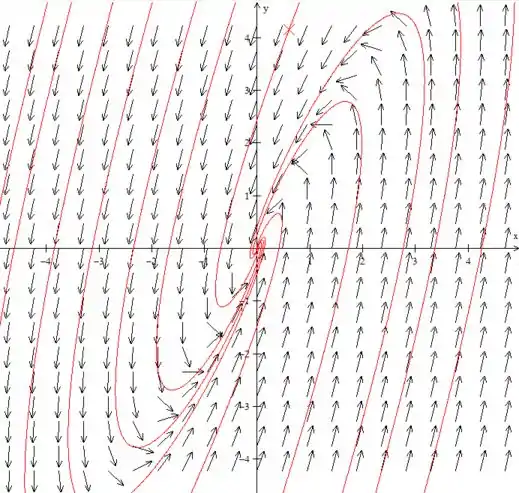
Quando t → ∞ tanto x 1 quanto x 2 tendem a zero.

Resposta

a )   x = c 1 cos ⁡ t 2 cos ⁡ t + s e n   t e - t + c 2 - s e n   t - 2   s e n   t + cos ⁡ t e - t

b )   I m a g e m   d o   P a s s o   3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em cada um dos problemas de 1 a 10 :(a) Encontre uma matriz fundamental para o sistema de equações dado.(b) Encontre, também, a matriz fundamental Φ ( t ) que satisfaz Φ ( 0 )=I . x ' = 1 - 1 5 - 3 x
Em cada um dos problemas de 1 a 10 :(a) Encontre uma matriz fundamental para o sistema de equações dado.(b) Encontre, também, a matriz fundamental Φ ( t ) que satisfaz Φ ( 0 )=I . x ' = 2 - 5 1 - 2 x
Em cada um dos problemas de 1 a 10 :(a) Encontre uma matriz fundamental para o sistema de equações dado.(b) Encontre, também, a matriz fundamental Φ ( t ) que satisfaz Φ ( 0 )=I . x ' = 2 - 1 3 - 2 x
A matriz fundamental Φ ( t ) para o sistema (3) foi encontrada no Exemplo 2. Mostre que Φ ( t ) Φ ( s )=Φ ( t+s ) multiplicando Φ ( t ) e Φ ( s ) .
Em cada um dos problemas de 1 a 10 :(a) Encontre uma matriz fundamental para o sistema de equações dado.(b) Encontre, também, a matriz fundamental Φ ( t ) que satisfaz Φ ( 0 )=I . x ' = - 1 - 4 1 - 1