Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 9.8 - Ex. 6
Em cada um dos problemas de 6 a 10, faça as investigações pedidas sobre as equações de Lorenz.
6. Para , faça o gráfico de em função de para os casos ilustrados nas Figuras 9.8.2 e 9.8.3. Seus gráficos são iguais aos das figuras? Lembre-se da discussão sobre cálculos numéricos no texto.
Passo 1
Bem, essa é uma questão o qual devemos desenvolver um programa que resolva o sistema que estamos trabalhando:
Com as condições semelhantes às condições usadas no desenho da figura 9.8.2 e 9.8.3.
Você pode programar em qualquer língua que tenha mais afinidade, lembrando-se dos conceitos de solução numérica de EDO. Aqui, eu optei por desenvolver em MATLAB, já que é uma língua simples, e com poucos códigos já obtemos a resposta.
Passo 2
Vou colocar aqui o meu código programado o qual você pode copiar e colar em um compilador da linguagem MATLAB. O código está todo comentado de modo que você possa compreender quando programei pra você, ok?
PRIMEIRO: defini essa função com informação das derivadas do nosso problema, onde :
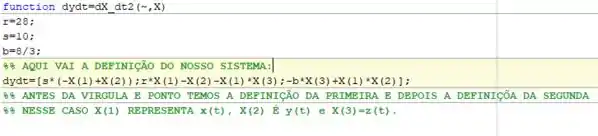
SEGUNDO: Criei o código que resolve essa derivada dando as condições iniciais (usei a função ode45 já desenvolvida no MATLAB):
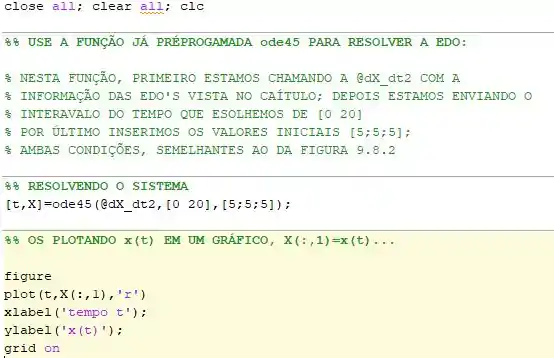
Perceba que o primeiro ponto inicial que adotei foi o ponto da figura 9.8.2: .
Quando iniciei a depuração do programa (coloquei pra rodar), ele me voltou esse gráfico:
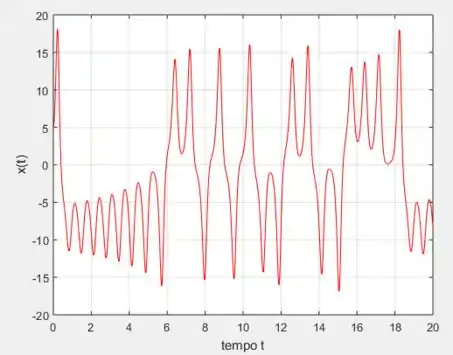
Comparando com o gráfico que o nosso amigo Boyce achou (gráfico 9.8.2):
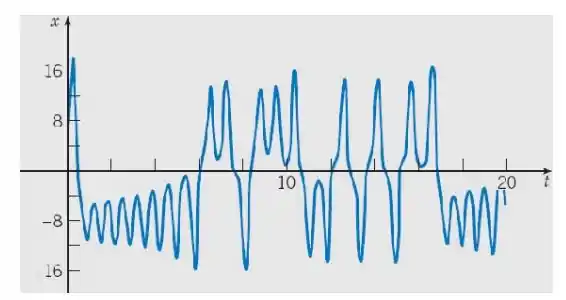
Repara que eles mantêm uma semelhança até aproximadamente . Depois eles começam a divergir bruscamente. Isso acontece por que a equação é extremamente sensível, dependendo, também, muito da precisão da máquina. Sendo o meu computador diferente do seu, é provável que as nossas soluções sejam diferentes, saca?
Passo 3
Agora vamos fazer a mesma coisa, mas para o gráfico 9.8.3, ou seja, aplicando a condição inicial (basta no código trocar para esse ponto inicial):
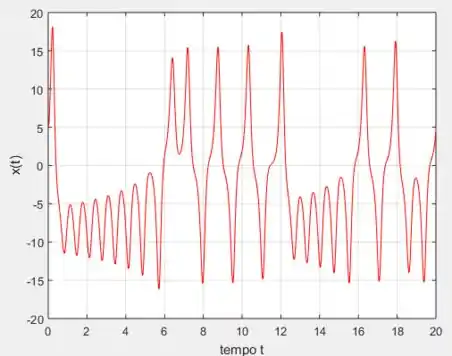
Comparando com a figura 9.8.3:
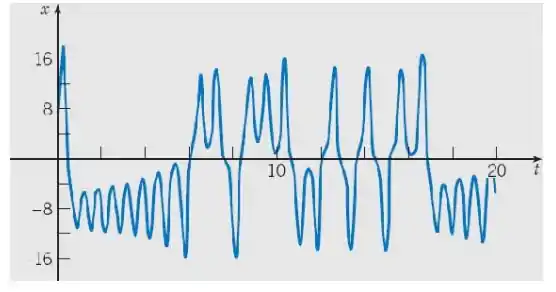
Segue a mesma coisa que já comentamos. São semelhantes até o .
Resposta
Ei, a resposta está no passo a passo :)