Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 7.6 - Ex. 28

Calcular a área da região sob o gráfico de y = 1 x 2 + 3 2 , de x = - 2 até x = 2 .

Passo 1

A área pedida é a da figura aqui:

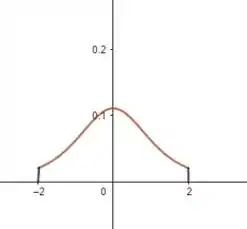
Passo 2

Pra calcular a área aqui é só a gente resolver a integral:

∫ - 2 2 1 x 2 + 3 2   d x

Aqui a gente pode fazer a substituição x = 3 t g   θ ,   d x = 3 sec 2 ⁡ θ d θ .

E aí x 2 + 3 = 3 t g 2   θ + 3 → 3 t g 2 θ + 1 = 3 sec 2 ⁡ θ .

Aí a nossa integral vira:

∫ 3 sec 2 ⁡ θ d θ 9 sec 4 ⁡ θ

Vamos resolver assim indefinida mesmo, depois a gente volta pra x e aplica os intervalos.

Passo 3

Simplificando, a gente fica com:

∫ 3 9 sec 2 ⁡ θ d θ

= 3 9 ∫ 1 sec 2 ⁡ θ d θ

= 3 9 ∫ cos 2 ⁡ θ   d θ

Aí integrando, fica:

3 9 1 2 θ + 1 4 s e n   2 θ + C

Tá, vamos voltar pra x agora...

θ = a r c t g x 3

s e n   2 θ = s e n   2 a r c t g x 3 = 2 3 3 + x 2

I = 3 9 1 2 a r c t g x 3 + 1 4 2 3 3 + x 2 - 2 2

Passo 4

Vamos aplicar os limites de integração agora:

I = 3 9 1 2 a r c t g 2 3 + 1 4 2 3 3 + 4 - 1 2 a r c t g - 2 3 - 1 4 2 3 7

= 3 9 a r c t g 2 3 + 2 21   u . a

Prontinho! Essa é a área pedida😉

Resposta

3 9 a r c t g 2 3 + 2 21   u . a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a Integral: ∫ x 2 x + 1 3 d x
Calcule a integral. ∫ d x x 3 + 2 x
Calcule a integral. ∫ 2 x 2 + 3 x + 3 x + 1 3 d x
Calcule a integral. ∫ x 3 - 2 x 2 + 2 x - 2 x 2 + 1 d x
Calcule a integral. ∫ x 3 + 3 x 2 + x + 9 x 2 + 1 ( x 2 + 3 ) d x