Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 7.6 - Ex. 26

Calcular a área da região sob o gráfico y = (1)/(x^2 + 2 x + 5) , de x = - 2 até x = 2 .

Passo 1

A área pedida é a da figura aqui:

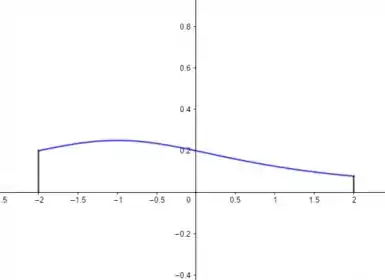
Passo 2

Pra calcular a área aqui é só a gente resolver a integral:

int_(- 2)^2 (1)/(x^2 + 2 x + 5) d x

A gente pode fatorar o denominador da fração, nesse caso a gente vai ter que completar o quadrado. Vai ficar assim:

int_(- 2)^2 (1)/((x - 1)^2 + 4) d x

Essa integral é a direta da arcotangente. Nesse caso:

[(1)/(2) a r c t g (x + 1)/(2)]_(- 2)^2

Passo 3

Agora a gente aplica os limites de integração:

(1)/(2) a r c t g (3)/(2) - (1)/(2) a r c t g - (1)/(2)

= (1)/(2) (a r c g t (3)/(2) - a r c t g (- (1)/(2))) u . a

Essa é a área procurada😉

Resposta

= (1)/(2) (a r c g t (3)/(2) - a r c t g (- (1)/(2))) u . a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta.Integrando em: ∫ 3 x 4 + 5 x 2 + 1 2 d x É uma função racional própria.
Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta. ‘Se f x = P x x + 5 3 for uma função racional própria, então a decomposição em frações parciais de f x tem termos com numera
Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta.A técnica das frações parciais é usada com integrais cujos integrandos são quocientes de polinômios.
Calcule a Integral:int (x^3 + x^2 + x + 2)/(( x^2 + 1 ) ( x^2 + 2 )) d x
Calcule a integral fazendo a substituição que converte o integrando em uma função racional. ∫ cos ⁡ θ sen 2 ⁡ θ + 4 sen ⁡ θ - 5 d θ