Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 9.2 - Ex. 15

Calcular as integrais curvilíneas.

∫ C x + | y |   d s , onde C   é o retângulo formado pelas retas x = 0 ,   x = 4 ,   y = - 1   e   y = 1 .

Passo 1

Vamos ver a região primeiro:

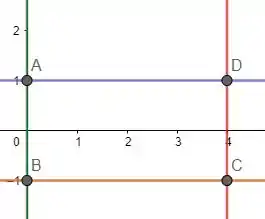
A região é esse retângulo de vértices A ,   B ,   C   e   D aí.

Vamos fazer 4 integrais de linha, uma por cada aresta do retângulo.

Pra isso, vamos escrever as retas que passam por dois vértices de cada vez.

Vamos chamar de C 1 ,   C 2 ,   C 3 e   C 4 , a integral procurada vai ser a soma dessas.

Passo 2

  • C 1 : r e t a   q u e   p a s s a   p o r   A   e   B :

    • A B → = 0 , - 2

    C 1 : x = 0 y = 1 - 2 t   ,   t ∈ 0,1

    Agora a gente deriva e faz a norma...

    C 1 ' =   - 2

    C 1 = - 2 2 = 2

    Vamos calcular a integral dessa de uma vez, como a função é modular, vamos ter que dividir na parte o 1 - 2 t é positiva e onde é negativa:

    ∫ 0 1 0 + 1 - 2 t   ( 2 ) d t

    ∫ 0 1 2 ( 1 - 2 t ) ( 2 )   d t + ∫ 1 2 1 2 t - 1 ( 2 )   d t

      2 t - 2 t 2 0 1 / 2 + 2 t 2 - 2 t 1 2 1

    = 1 - 1 2 + 2 - 2 - 1 2 + 1

    = 1

    Passo 3

    Vamos para a reta C 2 agora...

  • C 2 : r e t a   q u e   p a s s a   p o r   B   e   C :

    • B C → = 4,0

    C 2 : x = 4 t y = - 1 ,   t ∈ [ 0,1 ]

    Derivando essa parametrização, a gente encontra:

    4,0

    E fazendo a norma:

    C 2 ' = 4

    Vamos resolver a integral de linha aqui então...

    Aqui o módulo vai ser positivo quando t > 0 , então vai ser 1 só:

    ∫ 0 1 4 t + - 1   ( 4 ) d t

    ∫ 0 1 4 t + 1 ( 4 )   d t

    16 t 2 2 + 4 t 0 1 = 8 + 4 = 12

    Passo 4

    Vamos para a reta C 3 agora:

  • C 3 : r e t a   q u e   p a s s a   p o r   C   e   D …

    • C D → = 0,2

    C 3 : x = 4 y = - 1 + 2 t   ,   t ∈ [ 0,1 ]

    A derivada fica 0 ,   2 , e a norma:

    2 2 = 2

    Montando a integral agora...

    Lembrando que temos que dividir os intervalos onde a expressão do módulo é positiva e negativa...

    ∫ 0 1 2 ( 4 + 1 - 2 t ) 2 d t + ∫ 1 2 1 4 - 1 + 2 t 2 d t

    ∫ 0 1 / 2 5 - 2 t 2 d t + ∫ 1 2 1 ( 3 + 2 t ) ( 2 ) d t

    10 t - 2 t 2 0 1 2 + 6 t + 2 t 2 1 2 1

    = 5 - 1 2 + 6 + 2 - 3 - 1 2

    = 9

    Passo 5

    E agora a reta C 4 :

  • C 4 : r e t a   q u e   p a s s a   p o r   D   e   A

D A → = - 4,0

C 4 :   x = 4 - 4 t y = 1 ,   t ∈ [ 0,1 ]

Vamos fazer a derivada dessa parametrização agora:

C 4 ' = - 4,0

E a norma disso: C 4 ' = 4 .

Agora a gente monta a integral, aqui a gente tem que 4 - 4 t > 0 → t < 1 , então tá ok.

∫ 0 1 4 - 4 t + 1 4 d t

∫ 0 1 20 - 16 t   d t

  20 t - 16 t 2 2 0 1 = 20 - 8 = 1 2

Somando tudo agora, encontramos:

1 + 12 + 9 + 12 = 34

Resposta

3 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral de linha, onde C é a curva dada. ∫ C x y zd s C : x = 2s e nt ,y = t ,z =- 2 cos ⁡ t com 0 ≤ t ≤ π
Calcule a integral de linha, onde C é a curva dada. ∫ C x + 2 y d x + x 2 d y C consiste nos segmentos de reta de ( 0,0 ) a ( 2,1 ) e de ( 2,1 ) a ( 3,0 ) .
Calcule o valor da integral de linha, onde C é a curva dada.
Calcule a integral de linha, onde C é a curva dada. ∫ C y xd s C : x = t 4 ,y = t 3 , 1 2 ≤ t ≤ 1
Determine o valor exato de ∫ C x 3 y 5d s , onde C é a parte da astróide x = cos 3 ⁡ t , y = s e n 3 t no primeiro quadrante.