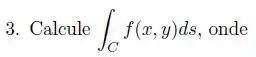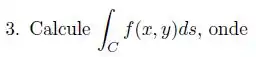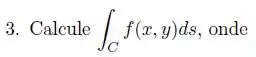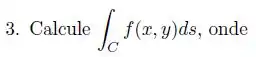Exercícios de Integral de Linha de Função Escalar no Plano - Lista de Exercícios Resolvida
Questão 1
Calcule a integral de linha da função escalar ao longo da curva parametrizada por
Ver solução completaQuestão 2
Seja a curva cujo traço é a parte da elipse no primeiro quadrante.
Calcule a massa de C, sendo a densidade .
Ver solução completaQuestão 3
Um pintor deseja pintar os dois lados de uma cerca cuja base é uma curva no plano dada por , para e . A altura em cada ponto é dada por . Se o pintor cobra reais por , quanto ele receberá?
Ver solução completaQuestão 4
- Calcule , ao longo dos seguintes caminhos fechados, orientados no sentido anti-horário.
- Triângulo de vértices e .
Ver solução completaQuestão 5
Calcule a massa da curva cujo traço é a parte da elipse no primeiro quadrante com densidade .
Ver solução completaQuestão 6
Calcule a integral de linha escalar , sendo a curva em dada por ligando os pontos e pelo arco de menor comprimento.
Ver solução completaQuestão 7
Sejam tais que . Considere a curva representada parametricamente por ,
b) Assuma . Usando a integral de linha, calcule o comprimento da curva
Ver solução completaQuestão 9
Calcule
b) é o arco da parábola x = 4 – y² de (−5, −3) até o ponto (0, 2).
Ver solução completaQuestão 10
Considere o campo vetorial F(x, y) = (3 + 2xy)i + (x² − 3y²)j.
(a) Encontre uma função f tal que F = ∇f;
Ver solução completaQuestão 11
Considere o campo vetorial
b) Calcule a integral de linha , onde C é a curva dada por
Ver solução completaQuestão 13
Considere a curva plana parametrizada por
- Faça um esboço da imagem/ traço de .
- Calcule a integral, com respeito ao comprimento do arco, da função escalar ao longo da curva parametrizada .
Questão 14
Calcule
Onde e é formada pelo arco da parábola de a seguido pelo segmento de reta vertical de a .
Ver solução completaQuestão 15
Um pintor deseja pintar os dois lados de uma cerca cuja base é uma curva no plano dada por , para e . A altura em cada ponto é dada por . Se o pintor cobra reais por , quanto ele receberá?
Ver solução completaQuestão 16
- Deseja-se construir uma peça de zinco que tem a forma da superfície do cilindro , compreendida entre os planos e , . Se o metro quadrado do zinco custa reais, calcule o preço total da peça.
Ver solução completaQuestão 17
Calcule a integral de linha escalar
Onde é a parte da curva entre os pontos e .
Ver solução completaQuestão 18
Seja a elipse percorrida no sentido anti-horário e apenas uma vez. O valor da integral é:
a)
b)
c)
d)
e)
Ver solução completaQuestão 19
(6) A integral da função escalar ao longo da curva parametrizada por
é igual a
Questão 20
- Calcule de a , ao longo
- do arco de circunferência , orientada no sentido anti-horário.
Ver solução completaQuestão 22
Calcule onde é a parte da curva dada por contida no primeiro quadrante, sendo .
Ver solução completaQuestão 23
Calcule a integral de linha de função escalar
ao longo da curva plana com parametrização dada por
Ver solução completaQuestão 25
Questão 3: Calcular a integral de linha da função escalar
Onde é a curva definida pela equação polar e situada no primeiro quadrante.
Ver solução completaQuestão 26
Calcule a Integral de Linha escalar , onde a curva tem equação , em coordenadas polares, com ponto inicial e ponto final
Ver solução completaQuestão 28
Calcule a integral de linha da função escalar ao longo da curva parametrizada por
Ver solução completaQuestão 29
- Calcule a massa da elipse , situada no primeiro quadrante, se a densidade em cada ponto é igual ao produto das coordenadas do ponto.
Ver solução completaQuestão 30
13. Calcule , onde é a interseção do paraboloide , com o plano ; o sentido de percurso deve ser escolhido de modo que a projeção de no plano caminhe no sentido anti-horário.
Ver solução completaQuestão 32
Considere a curva parametrizada por:
- Ache o elemento de comprimento de arco da curva parametrizada .
- Calcule o comprimento dessa curva
- Calcule
Questão 33
Calcule a integral de linha onde é a metade inferior da circunferência .
Ver solução completaQuestão 34
Um fio tem o formato da curva . Se sua densidade de massa é dada por , determine a massa total do fio.
Ver solução completaQuestão 39
Calcule a área de uma lado da superfície cuja base é a circunferência , no plano , e a altura em cada ponto é .
Ver solução completaQuestão 40
A figura mostra um campo vetorial e duas curvas, e . As integrais de linha de sobre e são positivas, negativas ou nulas? Explique.
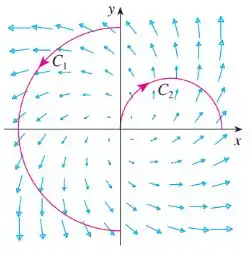
Questão 43
Sabendo que
Onde é a elipse
Calcule a área da região limitada pela elipse.
Ver solução completaQuestão 51
Uma partícula se move a o longo da parábola de tal forma que as componentes vertical e horizontal do vetor aceleração são sempre iguais. Se a partícula gasta 90s para ir do ponto à origem dos eixos, quanto tempo a mesma levará para ir do ponto P ao ponto ?
Ver solução completaQuestão 54
Seja a região do plano que é interior da região e o exterior da região . Se a denota a o bordo de , orientado positivamente, , podemos afirmar que:
Ver solução completaQuestão 57
Calcule a integral de linha, onde C é a curva dada
(b) , é o segmento de reta que liga
Ver solução completa