Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.2 - Ex. 3
Calcule o valor da integral de linha, onde é a metade é a metade do círculo
Passo 1
Fala , galera!
Nesse exercício vamos calcular a integral de linha:
Vamos precisar achar o valor de , calculando as derivadas parciais de pela fórmula:
Mas antes disso temos que fazer um passo muito importante que é a parametrização da curva , que é a metade direita do círculo .
Com essas informações poderemos resolver a integral!!
Passo 2
Vamos começar com a parametrização da curva . Como sabemos que se trata de um círculo iremos utilizar as coordenadas polares :
O exercício nos informa que a curva é metade direita do círculo:
Vamos relembrar um conceito importante. Representamos uma circunferência atrav��s da seguinte equação:
onde:
=Pontos do centro da circunferência
= raio
Quando a equação tem o formato: quer dizer que os pontos do centro da circunferência são (0,0)
Logo podemos afirmar que o raio da equação será 4:
Sendo assim, vamos substituir o valor do raio das equações paramétricas:
Beleza, outra análise que precisamos fazer da curva são os seus intervalos. A questão nos diz que a curva está à direita do círculo, sendo assim, se encontra no intervalo:
Relembrando o círculo trigonométrico: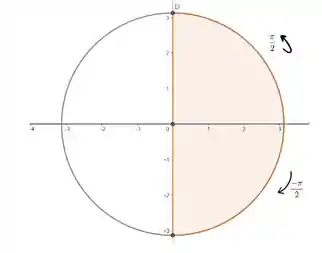 
Passo 3
Beleza, agora o próximo passo é substituir os novos valores de na função :
Sendo:
Logo:
Vamos reescrever a integral:
Passo 4
Show galera, agora só precisamos achar utilizando a fórmula:
lembrando que :
Então vamos calcular as derivadas parciais e :
Vamos substituir os valores na fórmula:
Colocando o 16 em evidência :
Lembrando que
Substituindo na integral:
↓
Passo 5
Agora, resolvendo a integral para , temos:
Tirando as constantes da integral:
Vamos resolver essa integral por substituição :
Substituindo na integral :
Dessa forma, o valor da integral é: