Calcular a integral tripla dada sobre a região indicada
Onde é o hemisfério da frente da esfera .
Passo 1
Fala pessoa! Tranquilidade? Vamos resolver mais uma questãozinha!
Dessa vez, o enunciao pede pra gente calcular a integral tripla:
Onde é o hemisfério da frente da esfera . Muita atenção na nomenclatura! “Parte da frente” da esfera é como se a gente cortasse a esfera na vertical e pegasse a “tigela” que sobrou. Dessa forma, temos uma região onde . Como estamos trabalhando com uma esfera, nada mais justo que a gente adote coordenadas esféricas para resolver o problemas. Sendo assim, temos que lembrar do seguinte:
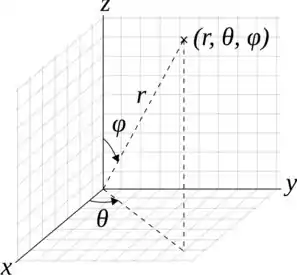
Com isso tudo em mente, vamos partir para a resolução!
Passo 2
O primeiro passo pra gente montar nossa integral é reescrever ela nas coordenadas esféricas. Vamos primeiro definir nossos limites de integração. Como estamos interessados na parte da frente da esfera, temos a região onde:
Ou seja:
Mas como sabemos, é naturalmente positivo. Isso nos faz concluir o seguinte:
Ainda podemos tirar uma conclusão bem interessante disso. O ângulo polar sempre é positivo. Isso por que, pela definição das coordenadas polares, ele varia da seguinte maneira:
Sendo assim, só nos resta a possibilidade de que:
Para essa condição, teremos “mapeado” a parte da frente do hemisfério. Ou seja, teremos que ter:
Além disso, nosso valor de tem os limites:
Isso por que a nossas expressão:
Nos dá o valor de:
Com todos esses ingredientes, vamos resolver o problema!!
Passo 3
Agora vamos montar nossa integral! Temos que converter o elemento de volume. Pela mudança de coordenadas, teremos o seguinte:
Para a mudança de coordenada, temos:
Substituindo na nossa integral, temos:
Vamos resolver com calma, de dentro para fora. Podemos ver que os limites de integração são bem definidos e não possuem dependência em nenhuma variável. Além disso, nosso integrando também não é dependente entre si. Podemos simplificar a integral da seguinte maneira:
Resolvendo cada uma, com calma, vamos ter o seguinte:
Avaliando nos limites de integração, temos:
Para a segunda integral, temos:
Avaliando nos limites de integração, temos:
Com isso, a segunda integral é:
Para a terceira integral, temos:
Avaliando a expressão, temos:
Passo 4
Juntando todas essas informações, temos que:
Substituindo o resultado que calculamos, temos:
Simplificando: