Enunciado
Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 5.11 - Ex. 2c
Calcule o volume do sólido descrito abaixo.
(c) é limitado pelas superfícies e , está situado no interior do cilindro e .
Passo 1
Faalaa aí Clóvis... Mais uma questãozinha nada trivial de integral tripla.
Como de praxe, vamos começar desenhando o diaxo do sólido para tentarmos enxergar o que tacoteseno.
Se você não ta conseguindo desenhar, lembra que a equação de um parabolóide que começa na origem é ?? Então se esse e forem negativos, o parabolóide será voltado para baixo a partir da origem.
Portanto, nada mais é do que um parabolóide voltado para baixo que não começa na origem, mas sim em .
E com a passagem de um plano, vamos ficar com o seguinte:
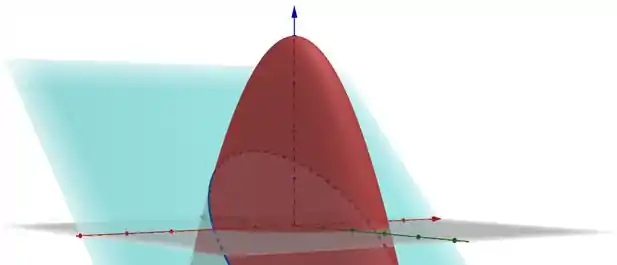
A linha tracejada em azul, representa a intersecção do plano com o parabolóide.
Mas, vamos ter que tomar muito cuidado com a interpretação. Digo isso porque num primeiro momento, pensei que o enunciado queria o volume daquilo que esta abaixo do plano .
Mas na verdade ele quer o que está acima; percebe que no final das contas queremos encontrar o volume do seguinte:
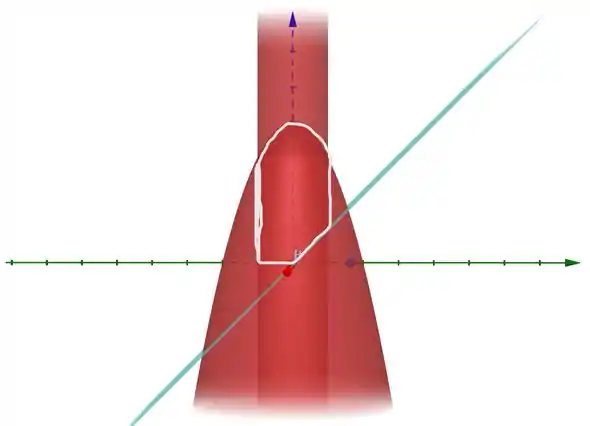
Queremos o que está em branco, limitado em cima pelo parabolóide, pelo plano em azul, pelo cilindro e ainda pelo plano .
Pegou a idéia?
Para proceder, podemos calcular o volume total e tirar daquele pedacinho que está abaixo do plano .
Para encontrar o volume total daquilo ali, é só calcular o volume do cilindro até a intersecção com a pontinha do parabolóide.
Ou seja,
Vamos ter que utilizar coordenadas cilíndricas; ah vá?! Cilindro, coordenadas cilíndricas... acho que tem alguma relação aí. Hahahaha
Relembrando:
Então para o cilindro, a projeção dele no plano forma uma circunferência. Com raio 1 e que pega todos os 4 quadrantes. Ou seja:
Mas falta os limites de ; perceba que, partindo da origem, subimos até a intersecção do cilindro com o parabolóide:
Mas , que é o cilindro.
Ou seja,
Passo 2
Então o volume do cilindro:
Lembrando sempre do jacobiano ali, pelo amor de tudo que é mais sagrado nesse mundo todinho...
Chegamos em:
E
Beleza, agora a pontinha do parabolóide.
A projeção, da intersecção do parabolóide com o cilindro, no plano também é uma circunferência de raio 1. E também pega os 4 quadrantes do plano . Portanto:
Só que agora,subindo no eixo , começamos em (intersecção) e continuamos subindo até encontrar com o parabolóide. Então:
Lembrando que . Certo??
Portanto o volume daquela pontinha la em cima:
Integrando:
Cuidado pra não errar:
Top demais, então temos que o volume total daquele rolê é:
Passo 3
Agora vamos falar daquela partinha que é excluída porque passamos um plano pelo sólido.
A projeção dela no plano é uma meia circunferência de raio 1. Consegue perceber isso?
Note que podemos excluir o parabolóide, e contar só a intersecção do plano com o cilindro:
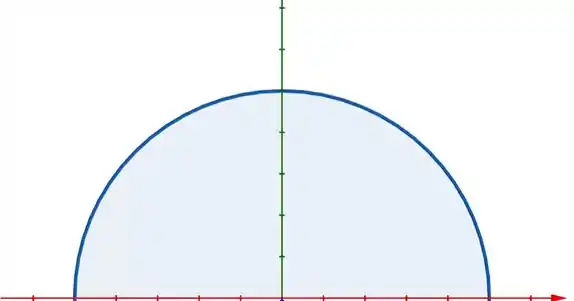
Mas diferente das projeções anteriores, temos somente uma meia circunferência que pega só os dois primeiros quadrantes:
E como ela possui raio 1:
Partindo do plano , perceba que podemos subir na direção de até encontrar com o plano ; portanto:
Mas, como estamos trabalhando com coordenadas cilíndricas:
Show dibola. Já temos todos os limites de integração.
O volume dessa brincadeira aí, será:
Integrando:
Um pouquinho de cuidado agora:
E finalmente:
Portanto:
Então, o volume do nosso sólido será:
Chegamos em:
Ufa!
Resposta
Concluimos que o volume do sólido limitado pelo parabolóide e pelo plano contidos no cilindro, é