Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 5.11 - Ex. 1a

Calcule a seguinte integral tripla:

∭ W z   d x   d y   d x

Onde, W é a região no primeiro octante limitada pelos planos y = 0 , z = 0 , x + y = 2 , 2 y + x = 6 e o cilindro y 2 + z 2 = 4 .

Passo 1

Bom, falou em cilindro não tem nem o que pensar; vamos ter que dar um jeito de aparecer corrdenadas cilíndricas aí.

Mas antes, vamos tentar visualizar o que está acontecendo:

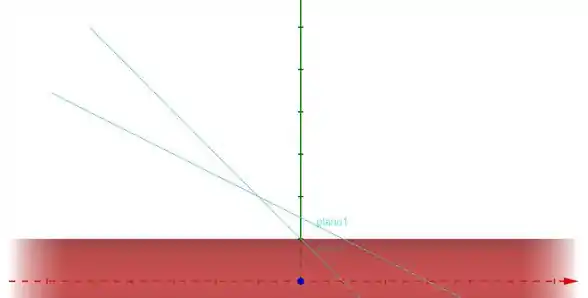
Olhando de cima temos isso aí... lembrando que temos que considerar só a parte de cima do eixo x (em vermelho). Isso porque a sólido é limitado também pelo plano y = 0 .

Tá, vamos fazer a mudança para as coordenadas cilíndricas.

Note que a projeção das duas intersecções no cilindro forma um quarto de uma circunferência no plano y z :

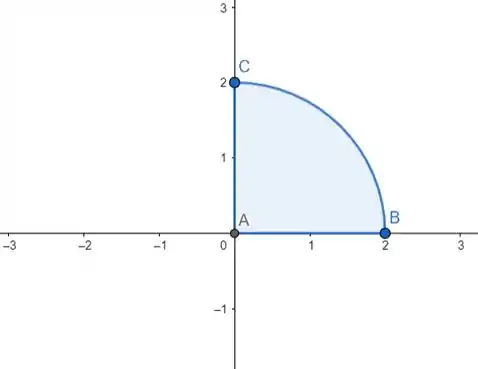
Pegou a idéia?

Passo 2

Vamos então fazer a mudança das variáveis para as coordenadas cilíndricas:

Como o cilindro está ao longo do eixo x , teremos o seguinte:

y = r cos ⁡ θ z = r sin ⁡ θ J a c o b i a n o = r   x = x

Bugou um bocado né; acontece que só alteramos os valores ali com y fazendo papel de x . Nada demais.

Perceba que o quarto da circunferência está no primeiro quadrante do plano, portanto:

0 ≤ θ ≤ π 2

E além disso ela é limita por um raio igual a 2:

0 ≤ r ≤ 2

Agora vamos ver como o x ta variando. Partindo de um ponto qualquer do plano z y e andando no sentido positivo do eixo x , primeiro nos deparamos com o plano 2 e em seguida com o plano 1 (de acordo com a primeira imagem la em cima).

Isso significa que:

2 - y ≤ x ≤ 6 - 2 y

Mas quem é o y mesmo?

2 - r cos ⁡ θ ≤ x ≤ 6 - 2 r cos ⁡ θ

Passo 3

Teremos a seguinte integral:

I = ∫ 0 π 2 ∫ 0 2 ∫ 2 - r cos ⁡ θ 6 - 2 r cos ⁡ θ r sin ⁡ θ   r   d x   d r   d θ

Não esquece de sempre multiplicar o o tio Jaco Biano alí.

I = ∫ 0 π 2 ∫ 0 2 r 2 sin ⁡ θ 6 - 2 r   c o s θ - 2 - r   c o s θ d r   d θ

Assusta um bocado; mas não é nada demais:

I = ∫ 0 π 2 ∫ 0 2 r 2 sin ⁡ θ 4 - r cos ⁡ θ   d r   d θ

Agora o r , podemos abrir em duas integrais:

I = ∫ 0 π 2 ∫ 0 2 4 r 2 sin ⁡ θ   d r d θ ⏟ I 1 - ∫ 0 π 2 ∫ 0 2 r 3 sin ⁡ θ cos ⁡ θ d r d θ ⏟ I 2

Melhor maneira é dividirmos em duas:

I 1 = ∫ 0 π 2 4 sin ⁡ θ   r 3 3 d θ r = 2 r = 0

E aí:

I 1 = ∫ 0 π 2 32 3 sin ⁡ θ d θ = 32 3 - cos ⁡ θ θ = π 2 θ = 0

Portanto:

I 1 = - 32 3 0 - 1 = 32 3

Beleza, agora a outra integral:

I 2 = ∫ 0 π 2 ∫ 0 2 r 3 sin ⁡ θ cos ⁡ θ d r d θ

I 2 = ∫ 0 π 2 sin ⁡ θ cos ⁡ θ r 4 4 d θ r = 2 r = 0

E portanto:

I 2 = 16 4 ∫ 0 π 2 sin ⁡ θ cos ⁡ θ d θ

Sem segredos, chamando u = cos ⁡ θ , d u = sin ⁡ θ d θ

Teremos:

I 2 = 4 cos 2 ⁡ θ 2 θ = π 2 θ = 0

Encontramos:

I 2 = 2

Então, nossa solução será:

I = 32 3 - 2 = 26 3

Showdibola! Até a próxima!!

Resposta

Encontramos a seguinte solução para a integral:

∭ W z   d x   d y   d x = 26 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o volume do sólido dado. Abaixo da superfície z = x 2 y e acima do triângulo no plano x y com vértices 1,0 ,2,1e4,0 .
Determine o volume do sólido dado. Uma das cunhas obtidas pelo corte do cilindro x 2 + 9 y 2 = a 2 pelos planos z = 0 e z = m x .
Uma luminária tem três lâmpadas, cada uma com vida média de 800h o r a s . Se modelarmos a probabilidade de falha das lâmpadas por uma função densidade exponencial com média 800 , determine a probabil
Utilize a transformação x = u 2 , y = v 2 , z = w 2 para determinar o volume da região limitada pela superfície x + y + z = 1 e pelos planos coordenados.
Use a integral tripla para determinar o volume do sólido dado.O sólido delimitado pelo cilindro y = x 2 e pelos planos z = 0 e y + z = 1