Enunciado
Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 5.11 - Ex. 2a
Calcule o volume do sólido descrito abaixo.
- é limitado pelo cone e o parabolóide .
Passo 1
Fala meu consagrado, vamos encontrar o volume desse rolê aqui.
Seguinte, sempre precisamos tentar enxergar quem raios são as superfícies que delimitam o sólido; então tenta desenhar isso daí:
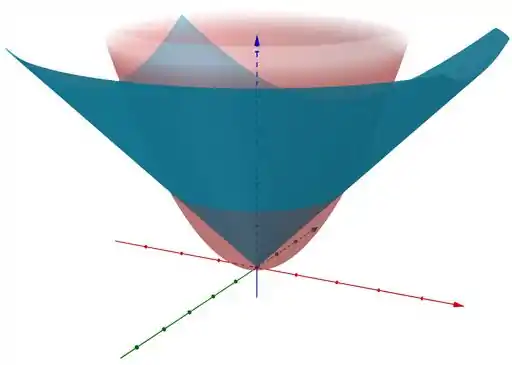
Eu sei que nada nessa matéria é fácil de enxergar, mas você consegue perceber que a intersecção dessas duas superfícies forma uma circunferência??
Essa intersecção é o que chamamos também de projeção no plano . Ou seja, ao olhar de cima, os pontos onde as duas superfícies se conectam formam uma circunferência.
Se ainda não estiver claro pra você, vamos tentar ver isso matematicamente; sendo a intersecção das superfícies:
Sumindo com a raíz:
E então:
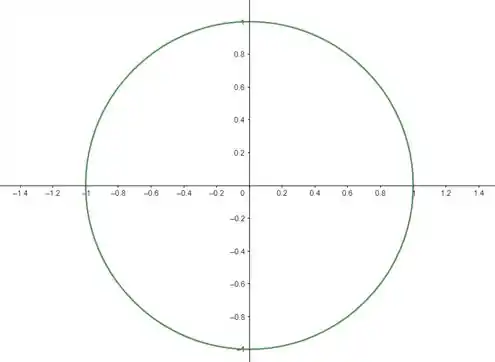
Ou seja, a projeção (intersecção) no plano é uma circunferência de raio 1.
Bom, vamos “plotar” essa circunferência para podermos transformar ela em coordenadas cilíndricas. Lembrando que sempre usamos a projeção para fazer essa análise.
Passo 2
Então agora vamos realizar essa mudança de variáveis para as coordenadas cilíndricas. Lembrando que:
Esses negocinhos aí tem que estar muito bem guardado na sua cabeça. Vamos usar isso aí praticamente o tempo inteiro.
Tendo relembrado isso, podemos fazer a transformação.
Olha na PROJEÇÃO e perceba que a circunferência pega os 4 quadrantes do plano. Portanto:
E note, que a projeção é limitada por um raio tamanho 1; ou seja:
Por último, dessa vez olhando para as superfícies (3D); saindo da origem vamos percorrer o eixo z. Percebeu que primeiro entramos na superfície que delimita o parabolóide? E continuando no eixo z encontramos a superfície .
Isso significa que:
Mas peraí... não podemos trabalhar com e porque queremos coordenadas cilíndricas, certo??
Certíssimo... então é só você lembrar que:
Sempre!!
Lembrando disso, chegamos à conclusão de que:
Pronto. Temos os três limites das integrais, basta substituir e integrar.
Passo 3
Então, temos a seguinte integral para o volume desse sólido:
Mas estamos trabalhando com coordenadas cilíndricas, então:
Lembre-se sempre de multiplicar o Tio Jaco Biano ali. Não quero nem pensar no que acontece se você esquecer disso...
E então aplicando os limites:
É só integrar:
E finalmente:
Tranquilo, né?!
Resposta
O volume do sólido é .