Enunciado
Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 5.11 - Ex. 2e
Calcule o volume do sólido descrito abaixo:
(e) .
Passo 1
Eaaaeeee, vamo chamar essa questão na xincha! Vem comigo...
O enunciado nos da algumas regiões ali, vamos tentar esboçar elas:
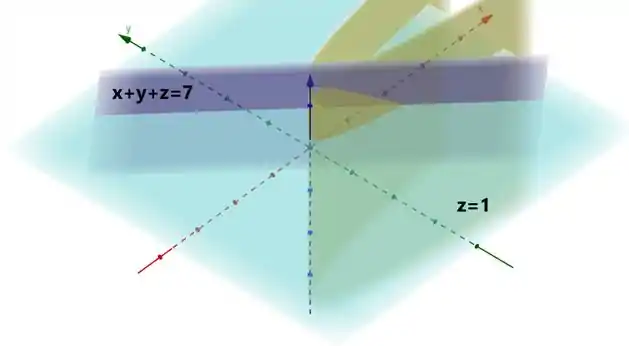
Achamos algo mais ou menos assim; onde aquela partinha em amarelo ali é o nosso sólido. Perceba que ele está limitado pela superfície (amarelo), e pelos planos e .
Bom, vamos ver como a projeção desse cara se comporta no plano ? É como se você tivesse vendo a figura de cima:
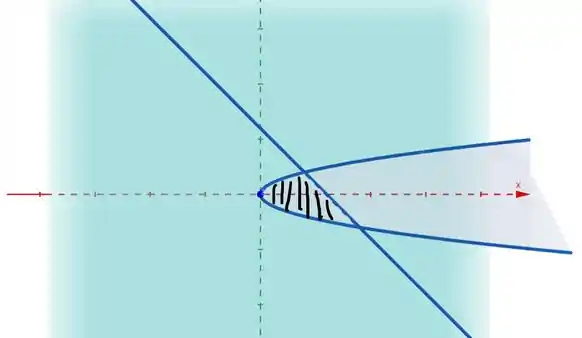
Teremos isso, onde a parte hachurada é quem nos interessa.
“huumm não sei não cara, não consigo enxergar isso...?!” Beleza, vou tentar te convencer utilizando a Tia Mat.
Essas projeções nada mais são do que as intersecções entre os bangs. Olha só:
Interceptando o plano , teremos:
Que é? Uma reta decrecente, isso mesmo:
Ela ta ali na imagem certo?
E agora a parábola?? É a
Sem segredos.
Passo 2
Tá, então vamos tentar determinar os limites da integração:
Perceba que o sai do plano até encontrar o plano , então teremos:
E o , repare que ele pode ser encontrado utilizando as intersecções:
Mas , então:
Portanto, os limites de serão:
Ou seja:
E por último o ; note que partindo da origem e saindo no sentido positivo do eixo , primeiro encontramos a parábola, e continuando no eixo depois encontramos a reta; ou seja:
Sacou a parada?
Passo 3
Então no final das contas o volume desse trem vai ser definido assim:
Certo?? Nããããooo.... Muito cuidado, mas muito cuidado mesmo com a ordenação dos diferenciais. Sempre de dentro pra fora, olha só:
Agooraa siiimm... Let’s bora:
A próxima:
Vamos abrir isso tudo em somas, olha só:
Meu pai amado...
Horrível né, eu sei! Mas vamos juntos, com calma para não errar nada:
Agora integrando:
Bom, vamos analisar separadamente, se tivermos:
Caso esteja elevado a uma potência par:
Caso seja ímpar:
Pegou a ideia?? Com esse raciocínio, vamos aplicar os limites então:
Conversa com a calculadora aí, faz carinho e pede para que ela gentilmente te mostre que:
Achou aí?? Terminamos então... see you.
Resposta
Concluimos que o volume do sólido é: