Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 3.5 - Ex. 4a

Calcule a área da intersecção da região limitada pelas curvas dadas em coordenadas polares

a )   ρ = 2 - cos ⁡ θ   e   ρ = 1 + cos ⁡ θ

Passo 1

Primeiro devemos descobrir onde elas se intersectam:

2 - cos ⁡ θ = 1 + cos ⁡ θ → 1 = 2 cos ⁡ θ → θ = cos - 1 ⁡ 1 2

Pegando o ciclo trigonométrico vamos ver que os ângulos que atendem a esse valor são 5 π 3 e π 3

Podemos usar também - π 3   e π 3 .

Se fizermos os desenhos das duas curvas, vamos ficar com algo assim:

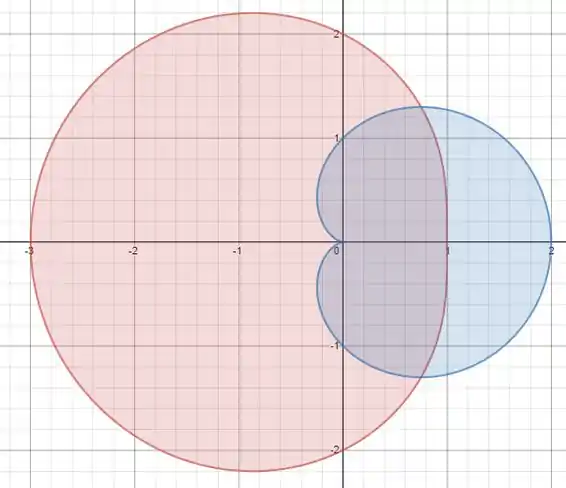
Dá pra ver que se intersectam justo nos ângulos encontrados, para fazer o cálculo da área de intersecção precisamos calcular uma área relativa apenas a um e outra relativa apenas a outra pra ficar fácil de calcular, nesse caso.

Se chamarmos a área a esquerda de Área 1 e a área dá direita de Área 2, usaremos para a área 2 o intervalo de π 3 , 5 π 3 e para a Área 1 vamos usar o intervalo 5 π 3 , π 3 , porém para ficar mais fácil de enxergar vamos adotar o intervalo - π 3 , π 3 .

Vamos ter uma imagem assim:

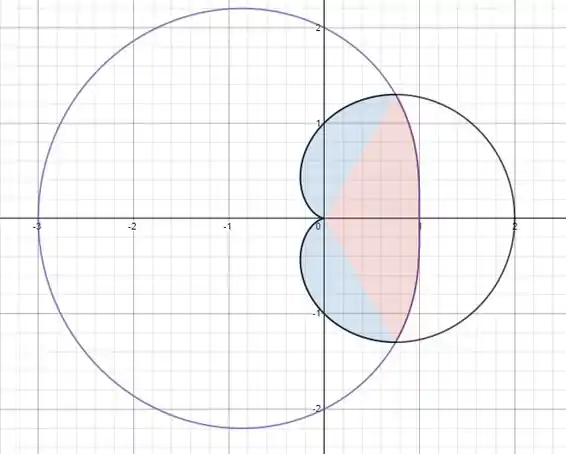
Passo 2

Agora vamos lembrar que a área em coordenadas polares pode ser descrita assim:

Á r e a = 1 2 ∫ α β ρ 2 d θ

Para tirar esse 1 2 vamos fazer o seguinte: Dá pra ver pela figura que a imagem é simétrica em relação ao eixo Ox, ou seja, podemos multiplicar só por uma das partes, usar metade do intervalo e depois multiplicar o área por 2, assim:

Á r e a   1 = 2 × 1 2 ∫ 0 π 3 2 - cos ⁡ θ 2 d θ = ∫ 0 π 3 4 - 4 cos ⁡ θ + cos 2 ⁡ θ d θ

Á r e a   2 = 2 × 1 2 ∫ π 3 π 1 + cos ⁡ θ d θ = ∫ π 3 π 1 + 2 cos ⁡ θ + cos 2 ⁡ θ d θ

Vamos aos cálculos!

Passo 3

Á r e a   1 = ∫ 0 π 3 4 - 4 cos ⁡ θ + cos 2 ⁡ θ d θ = ∫ 0 π 3 4 d θ - ∫ 0 π 3 4 cos ⁡ θ d θ + ∫ 0 π 3 cos 2 ⁡ θ d θ =

Vamos substituir cos 2 ⁡ θ = 1 2 1 + cos ⁡ 2 θ e depois aplicaremos   u = 2 θ → d u = 2 d θ

4 π 3 - 4 sin ⁡ θ π 3 0 + ∫ 0 π 3 1 2 1 + cos ⁡ 2 θ d θ = 4 π 3 - 4 3 2 + ∫ 0 π 3 1 2 1 + cos ⁡ 2 θ d θ

4 π 3 - 4 3 2 + 1 4 ∫ 0 2 π 3 1 + cos ⁡ u d u = 4 π 3 - 4 3 2 + 1 4 u + sin ⁡ u 2 π 3 0

= 4 π 3 - 4 3 2 + 1 4 2 π 3 + 3 2 = 8 π + π 6 - 16 3 + 3 8 = 9 π 6 - 15 3 8

Á r e a   2 = ∫ π 3 π 1 + 2 cos ⁡ θ + cos 2 ⁡ θ d θ = ∫ π 3 π 1 d θ + ∫ π 3 π 2 cos ⁡ θ d θ + ∫ π 3 π cos 2 ⁡ θ d θ =

Vamos aplicar aqui a mesma substituição feita em cima

π - π 3 + 2 sin ⁡ θ π π 3 + ∫ π 3 π 1 2 1 + cos ⁡ 2 θ d θ = 2 π 3 + 2 - 3 2 + 1 4 ∫ 2 π 3 2 π 1 + cos ⁡ u d u =

= 2 π 3 + 2 - 3 2 + 1 4 u + s e n u 2 π 2 π 3 = 2 π 3 - 3 + 1 4 2 π - 2 π 3 + 0 - 3 2 =

= 2 π 3 - 3 + 1 4 6 π - 2 π 3 - 3 2 = 2 π 3 - 3 + 4 π 12 - 3 8 = 2 π + π 3 - 8 3 - 3 8 =

= π - 9 3 8

Agora somamos:

9 π 6 - 15 3 8 + π - 9 3 8 = 15 π 6 - 24 3 8 = 5 π 2 - 3 3

Resposta

Á r e a = ∫ 0 π 3 4 - 4 cos ⁡ θ + cos 2 ⁡ θ d θ + ∫ π 3 π 1 + 2 cos ⁡ θ + cos 2 ⁡ θ d θ = 5 π 2 - 3 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta. Cada afirmação se refere a uma partícula em movimento retilíneo.Se a área total entre o gráfico da velocidade versus tempo e
Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta. Cada afirmação se refere a uma partícula em movimento retilíneo.Se D ( t ) denotar a distância percorrida pela partícula no
Para cada função velocidade v ( t ) dada:Gere a curva velocidade versus tempo e use-a para fazer uma conjectura sobre o sinal do deslocamento sobre os intervalos de tempo dados.Use um CAS para encontr
Para cada função velocidade v ( t ) dada:Gere a curva velocidade versus tempo e use-a para fazer uma conjectura sobre o sinal do deslocamento sobre os intervalos de tempo dados.Use um CAS para encontr
Para cada função velocidade v ( t ) dada:Gere a curva velocidade versus tempo e use-a para fazer uma conjectura sobre o sinal do deslocamento sobre os intervalos de tempo dados.Use um CAS para encontr