Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 3.2 - Ex. 1c

Calcule o volume do sólido obtido pela rotação, em torno do eixo y, do conjunto de todos os (x, y) tais que

1 ≤ x ≤ 2     e 0 ≤ y ≤ x 3 - 1

Passo 1

Primeiro vamos entender o que se passa e o que se pede analisando o gráfico abaixo:

F u n ç ã o   y = x 3 - 1 ,   c o m   1 ≤ x ≤ 2

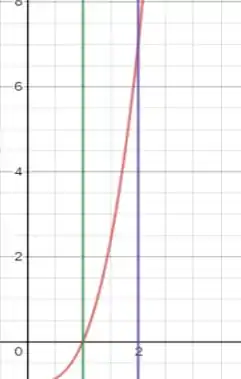
Vamos criar pequenos retângulos entre o eixo x e o x 3 - 1 com largura infinitesimal (que poderemos aproximar para dx) e rotacionar esse relangulo em volta do eixo x criando cilindros.

Analisando o gráfico, você descobre que o raio desses Cilindros é sempre a distância entre o eixo y e o valor de x avaliado no meio do dx.

Sabemos que o volume desses cilindros é: 2 π r × h × l , sendo que l é espessura do cilindro (que vimos ser dx), h vai ser a distância entre x 3 - 1 e 0 (que é o próprio x 3 - 1 ) e r é a distância do eixo y até o x (que vai ser sempre x, nesse caso).

Assim, somando todos esses cilindros teremos:

∫ 2 π x × ( x 3 - 1 ) × d x

E como o exercício diz que o conjunto tem x variando de 1 a 2 temos também os limites de integração

∫ 1 2 2 π x × ( x 3 - 1 ) × d x

Mãos a massa!

Passo 2

∫ 1 2 2 π x × ( x 3 - 1 ) × d x

Podemos reescrever como:

2 π ∫ x 4 - x d x = 2 π x 5 5 - x 2 2 + c

Passo 3

Agora aplicamos os limites de integração:

2 π ∫ 1 2 x 4 - x d x =   2 π x 5 5 - x 2 2 + c 2 1 = 2 π 2 5 5 - 2 2 2 + c - 1 5 5 - 1 2 2 + c =

= 2 π 2 6 - 2 2 × 5 - 2 + 5 10 = π 64 - 20 - 2 + 5 5 = π 47 5

Resposta

V = ∫ 1 2 2 π x × ( x 3 - 1 ) × d x = π 47 5

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule o volume do sólido obtido pela rotação, em torno do eixo y, do conjunto de todos os (x, y) tais que 0 ≤ x ≤ 1 e 0 ≤ y ≤ tan - 1 ⁡ x
(Volume de Sólido de revolução em torno do eixo y). Suponha f Estritamente crescente e com derivada contínua em [ a ,b ] , a ≥ 0ef a = 0 . Seja g : 0 , f b → a ,b A função inversa de f .Verifique que
Calcule o volume do sólido obtido pela rotação, em torno do eixo y, do conjunto de todos os (x, y) tais que 0 ≤ x ≤ 2 , y ≥ x - 1 e 0 ≤ y ≤ x 2
Calcule o volume do sólido obtido pela rotação, em torno do eixo y, do conjunto de todos os (x, y) tais que y 2 ≤ 2 x - x 2 , y ≥ 0
Calcule o volume do sólido cuja base é o quadrado de vértices (0,0),(0,1),(1,0) e (1,1) e cujas secções perpendiculares ao eixo Ox são triângulos isósceles de altura x-x².