Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 8.2 - Ex. 9

9) Calcule a área da região limitada pela reta y = x e pela curva x   =   t 3   +   t e y   =   t 5   +   t , com 0 ≤ t ≤ 1. Desenhe a região.

Passo 1

A região que queremos calcular é essa abaixo, entre as curvas

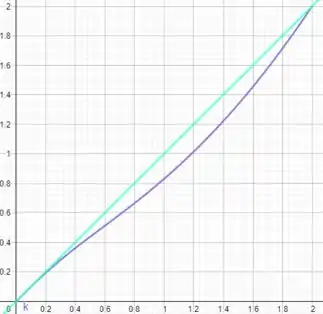
Para calcular essa região podemos usar a dica do exercício 1

k =   ∮ γ x   d y  

Passo 2

No nosso caso teremos que desmembrar em duas curvas

k =   ∮ γ 1 x 1   d y   +   ∮ γ 2 x 2   d y  

Vamos definir γ 1 como

x   =   t 3     +   t   y   =   t 5     +   t

  0   ≤   t   ≤   1

d y = ( 5 t 4 + 1 )   d t

E vamos também definir γ 2   c o m o  

y   =   x = t

  0   ≤   t   ≤   2

d y = d t

Passo 3

Vamos unir esses cálculos à nossa integração. Lembrando que a reta y = x tem que completar a circulação, ou seja, está no sentido anti-horario

k =   ∮ 0 1 ( t 3     +   t   ) ( 5 t 4 + 1 )   d t   +   ∮ 2 0 t   d t  

k =   ∮ 0 1 5 t 7 + 5 t 5 + t 3 + t   d t   + t 2 2 2 0  

k = 5 8 t 8 + 5 6 t 6 + t 4 4 + t 2 2 0 1   + t 2 2 2 0

k = 5 8 + 5 6 + 1 4 + 1 2 - 2 = 5 24

Terminamos por aqui. Te vejo na próxima resolução

: )

Resposta

∮ γ x   d y   = 5 24

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

5) Calcule ∮ γ Fd γ onde F x , y = 4 x 3 y 3 i + 3 x 4 y 2 + 5 x j e γ é a fronteira do quadradro de vértices (-1,0), (0,-1), (1,0),(0,1)
1 ) Sejam γ e K como no teorema de Green. Prove que área de k =∮ γ xd y
4 ) Calcule ∮ γ Fd γ onde γ é uma curva fechada, simples, C 1 por partes, cuja imagem é a fronteira de um compacto B e Fx , y= 2 x + y i + 3 x - y j
3) Calcule a área da região limitada pela elipse x = a cos t, y = b sen t, 0 ≤ t ≤2π, onde a0 e b0.