Enunciado
Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 7.3 - Ex. 3
3 ) Seja Ω = {(x, y) ∈ ℝ2 | (x, y) ∉ A}, onde A é a semirreta {(x, y)∈ ℝ2 | y= 0 e x ≥ 0}. Calcule
onde é uma curva C1 por partes, com imagem contida em Ω, talque
Passo 1
Esse exercício é continuação do exercício resolvido 1-f. Temos aqui a mesma função com restrições diferentes. Desta vez não podemos Atravessar direto do 1º quadrante para o 4º quadrante. Teremos que fazer curvas para isso.
No exercício 1-f fizemos essa curva
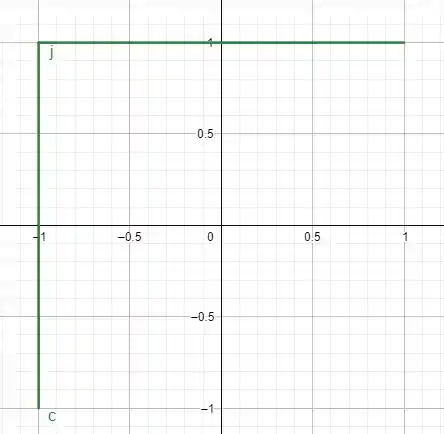
Proponho a seguinte curva agora
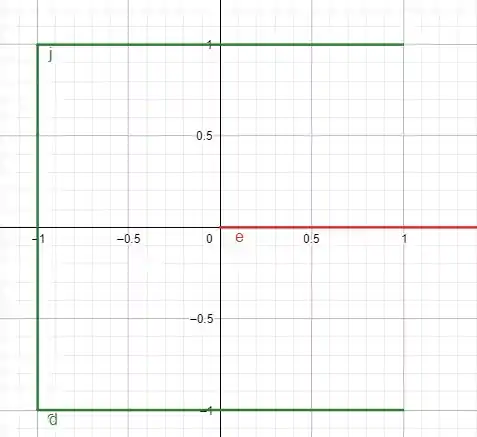
Adicionar a curva horizontal inferior, visto que a reta em vermelha esta fora do nosso domínio, impossibilitando que tracemos uma linha vertical direta entre e
Passo 2
Nosso calculo consiste em parametrizar nossa função F e calcular
Proponho como parametrização
Assim nossa fica
Passo 3
Vamos calcular essa integral agora
Agora vamos adicionar esse valor com o resultado do item 1-f
Logo temos
Terminamos por aqui. Te vejo na próxima resolução
: )