Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.5 - Ex. 64

a) Calcule a área da superfície da elipsoide que é gerada ao rotacionar a elipse em torno do seu eixo maior.

b) Qual é a área da superfície se a elipse for rotacionada em seu eixo menor?

Passo 1

Olá, meu amigo. Pronto para aprender mais um pouco hoje? Vou te ajudar na resolução dessa atividade.

O problema pede para encontrarmos a área da superfície obtido ao rotacionarmos uma elipse em torno do seu eixo maior. Vamos considerar que esse eixo seja o eixo x :

x 2 a 2 + y 2 b 2 = 1

Temos, portanto, a > b . A seguir plotamos a metade superior da elipse que será girada em torno do eixo x :

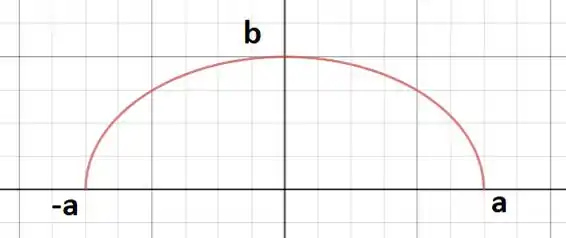
Vimos durante nossos estudos que a área da superfície de um sólido obtido pela revolução em torno do eixo x é

A = 2 π   ∫ y d s

Vamos usar coordenadas polares para fazer essa integral! A equação da elipse pode ser escrita como

x = a cos ⁡ θ   ;   y = b sin ⁡ θ

E

0 < θ < π

Assim como:

d s = d x 2 + d y 2

Passo 2

Primeira coisa que deveremos fazer é continuar o desenvolvimento de d s .

Temos então que:

d s = d x d θ 2 + d y d θ 2

Derivando:

d s = - a sin ⁡ θ 2 + b cos ⁡ θ 2

d s = a 2 sin 2 ⁡ θ + b 2 cos 2 ⁡ θ

Agora a gente parte para a montagem e solução da nossa integral:

S = 2 π ∫ 0 2 π b sin ⁡ θ a 2 sin 2 ⁡ θ + b 2 cos 2 ⁡ θ d θ

Utilizando da identidade trigonométrica fundamental iremos reescrever:

S = 2 π ∫ 0 2 π b sin ⁡ θ a 2 - a 2 cos 2 ⁡ θ + b 2 cos 2 ⁡ θ d θ

Colocando em evidência:

S = 2 π ∫ 0 2 π b sin ⁡ θ a 2 + b 2 - a 2 cos 2 ⁡ θ d θ

Iremos agora utilizar de uma substituição trigonométrica cos ⁡ θ = u e - sin ⁡ θ d θ = d u :

S = - 2 π b ∫ 1 - 1 a 2 + b 2 - a 2 u 2 d u

Podemos mudar os limites de integral multiplicando a integral por - 1 :

S = 2 π b ∫ - 1 1 a 2 + b 2 - a 2 u 2 d u

Assim como podemos multiplicar a nossa integral por 2 e por ela ser simétrica e mudarmos os limites de integração:

S = 2 π b ∫ 0 1 a 2 + b 2 - a 2 u 2 d u

Lembre-se que a 2 - b 2 = a 2 e 2

S = 4 π b ∫ 0 1 a 2 - a 2 e 2 u 2 d u

S = 4 π a b e ∫ 0 1 1 e 2 - u 2 d u

Passo 3

Essa integral é tabelada, irei te relembrar:

∫ a 2 - u 2 d u = u 2 a 2 - u 2 + a 2 2 sin - 1 ⁡ u a + C

S = 4 π a b e u 2 1 e 2 - u 2 + 1 e 2 2 sin - 1 ⁡ u 1 e 0 1

Colocando os limites de integração:

S = 4 π a b e 1 2 1 e 2 - 1 + 1 2 e 2 sin - 1 ⁡ e

Organizando tudo:

S = 4 π a b e 1 - e 2 2 e + 1 2 e 2 sin - 1 ⁡ e

S = 4 π a b e b 2 a e + 1 2 e 2 sin - 1 ⁡ e

S = 2 π a b b a + 1 e sin - 1 ⁡ e

Passo 4

b) Agora a quer girar da seguinte forma:

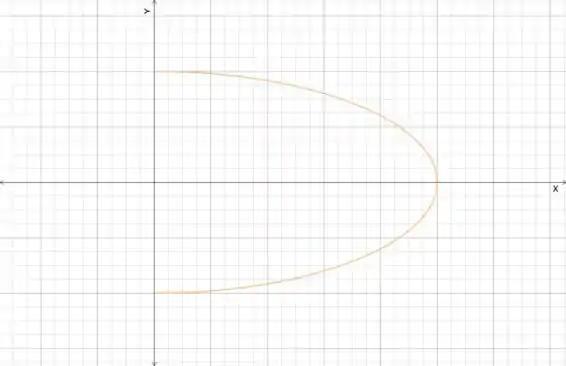
Com o intervalo de:

x = a cos ⁡ θ

y = b sin ⁡ θ

- π 2 < θ < π 2

E a integral se torna:

S = ∫ a b 2 π x d s

Vamos calcular então o nosso d s .

d s = ( d x ) 2 + ( d y ) 2

d s = d x d θ 2 + d y d θ 2

Derivando:

d s = [ - a s i n ⁡ θ ] 2 + [ b c o s ⁡ θ ] 2

Temos então:

d s = a 2 s i n 2 ⁡ θ + b 2 c o s 2 ⁡ θ

Agora a gente pode montar e calcular a nossa integral.

Passo 5

Montando a nossa integral:

S = 2 π ∫ - π 2 π 2   acos ⁡ θ a 2 sin 2 ⁡ θ + b 2 cos 2 ⁡ θ d θ

Utilizando da identidade trigonométrica fundamental:

S = 2 π ∫ - π 2 π 2   acos ⁡ θ a 2 sin 2 ⁡ θ + b 2 - b 2 sin 2 ⁡ θ d θ

Colocando em evidência:

S = 2 π ∫ - π 2 π 2   acos ⁡ θ a 2 - b 2 sin 2 ⁡ θ + b 2 d θ

Iremos utilizar de uma substituição trigonométrica sin ⁡ θ = u e cos ⁡ θ d θ = d u

S = 2 π a ∫ - 1 1   a 2 - b 2 u 2 + b 2 d u

Podemos então multiplicar a nossa integral por 2 e mudar os limites pois ela é simétrica.

S = 4 π a ∫ 0 1   a 2 - b 2 u 2 + b 2 d u

S = 4 π a a 2 - b 2 ∫ 0 1   u 2 + b 2 a 2 - b 2 d u

Lembre-se   a 2 - b 2 = a e :

Então:

S = 4 π a 2 e ∫ 0 1   u 2 + ( b / a e ) 2 d u

Passo 6

Para resolvermos essa integral deveremos utilizar da integral tabelada:

∫ a 2 + u 2 d u = u 2 a 2 + u 2 + a 2 2 ln ⁡ u + u 2 + a 2 + C

Resolvendo a nossa integral:

S = 4 π a 2 e u 2 ( b / a e ) 2 + u 2 + ( b / a e ) 2 2 ln ⁡ u + u 2 + ( b / a e ) 2 0 1

Colocando os limites de integração:

S = 4 π a 2 e 1 2 ( b / a e ) 2 + 1 + ( b / a e ) 2 2 ln ⁡ 1 + 1 + ( b / a e ) 2 - 4 π a 2 e ( b / a e ) 2 2 ln ⁡ b a e

Simplificando:

S = 4 π a 2 e 1 2 a e b 2 + a 2 e 2 + b 2 2 a 2 e 2 ln ⁡ a e b + 1 b a 2 e 2 + b 2

Simplificando mais ainda:

S = 4 π a 2 e 1 2 e + b 2 2 a 2 e 2 ln ⁡ a e b + a b

S = 2 π a 2 + b 2 e ln ⁡ e + 1 b a

Como a 2 - b 2 = a e ,   podemos escrever então como:

S = 2 π a 2 + b 2 e ln ⁡ 1 + e 1 - e 2

Resposta

  1. S = 2 π a b b a + 1 e sin - 1 ⁡ e

S = 2 π a 2 + b 2 e ln ⁡ 1 + e 1 - e 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre os vértices e os focos da elipse e esboce seu gráfico: 9 x 2 - 18 x + 4 y 2 = 27
Encontre o vértice, o foco, e a diretriz da parábola e esboce o seu gráfico.6. ( y - 2 ) 2 = 2 x + 1
Encontre os vértices, os focos e as assíntotas da hipérbole e esboce seu gráfico: 9 y 2 - 4 x 2 - 36 y - 8 x = 4
Encontre o vértice, o foco, e a diretriz da parábola e esboce o seu gráfico. 2 x 2 - 16 x - 3 y + 38 = 0
Encontre a equação para a cônica que satisfaz as condições dadas.33. Parábola, foco ( - 4 ,0 ) , diretriz x = 2 .