Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.5 - Ex. 24
Encontre os vértices, os focos e as assíntotas da hipérbole e esboce seu gráfico:
Passo 1
Eaee, belezinha?? Bom... o enunciado nos deu a seguinte equação que descreve uma hipérbole:
Queremos encontrar os vértices, os focos e as assíntotas da hipérbole. Mas o que são eles??
Bom... para respondermos isso temos que analisar a figura da hipérbole abaixo:
Nessa figura temos que:
- e são os focos;
- e são os vértices;
- As retas pontilhadas são as assíntotas;
- A distância do centro a um dos focos é dada por ;
- A distância do centro a um dos vértices é dada por ;
- A distância do centro a um dos conjugados é dada por .
Temos também que:
Também sabemos que a equação geral que descreve uma hipérbole centrada na origem é dada por:
Agora bora aplicar!! 😉
Passo 2
Precisamos deixar a equação dada na forma padrão da hipérbole.
Para isso, primeiro começamos somando para que possamos completar quadrados depois:
Completamos primeiro para :
E agora subtraímos para podermos completar para :
Primeiro fazemos fator comum novamente:
E completamos:
Por fim, dividimos dos dois lados por :
Vamos ter cuidado:
- O negativo começando nossa equação aí quer dizer que a nossa parábola está invertida (imagine girar em a figura mostrada no passo 1);
- perceba que o significa dizer que a figura está duas unidades movidas para cima.
- Além disso, o significa que nossa figura está movida para a esquerda em uma unidade.
Passo 3
Podemos agora calcular e :
E
E com os resultados, calcular :
Passo 4
Pela definição dos vértices de dos focos, podemos encontrar suas coordenadas, precisamos apenas tomar cuidado com os termos que estão somando ou subtraindo e na equação da hipérbole, pois correspondem a translações, então teremos para os vértices:
e
E para os focos:
As assíntotas serão:
Assim, o gráfico dessa hipérbole será:
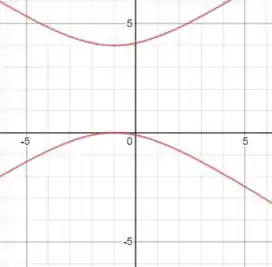
Resposta
Vértices:
e
Focos:
Assíntotas:
