Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.4 - Ex. 16
Uma lâmina ocupa a região dentro do círculo mas fora do círculo . Encontre o centro de massa se a densidade em qualquer ponto for inversamente proporcional à sua distância da origem.
Passo 1
Fala, pessoal! De boa?
Galera, conforme o exercício nos descreve, a lâmina deve ser assim:
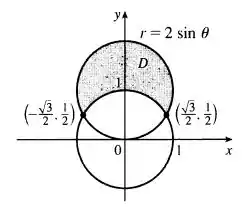
círculos (cinza) e (branco)
Para esboçar esse gráfico fazemos um círculo com centro na origem e raio 1. O outro círculo conseguimos igualando as duas equações
e
e obtendo:
E substituindo esse valor em qualquer uma das duas equações:
O centro de massa é um ponto com coordenada:
E o valor dessas coordenas a gente consegue calculando as seguintes integrais duplas:
Onde são os momentos em torno de cada eixo:
E:
Aqui, nossa variável se refere a massa dessa lâmina, que a gente vai precisar calcular pela integral:
Então, vamos usar a descrição da lâmina para encontrar nossos limites de integração das nossas integrais, resolver a integral da massa para finalmente conseguirmos substituir nas integrais de e para calculá-las. Também vamos precisar encontrar nossa função densidade .
Como estamos lidando com regiões circulares, vamos usar coordenadas polares para facilitar nossa descrição da região de integração. Para esse sistema, temos:
Vamos lá!
Passo 2
Vamos começar definindo nossa função densidade . O enunciado diz que a densidade em qualquer ponto for inversamente proporcional à sua distância da origem.
A distância de um ponto até a origem pode ser dada pela equação:
Se a densidade é inversamente proporcional à distância, ou seja, quando a densidade aumenta, a distância diminui e vice versa, podemos escrever:
Aqui, é uma constante de proporcionalidade. A gente não pode esquecer que estamos trabalhando com coordenadas polares, então, usando:
Substituindo:
Passo 3
Agora podemos achar nossos limites de integração das nossas integrais:
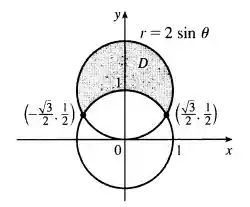
Olhando para a variação de que é medido no sentido anti-horário a partir da parte positiva do eixo , temos:
Já que nossa região começa ocupando 1/3 do primeiro quadrante e termina ocupando o primeiro quadrante inteiro mais 2/3 do segundo quadrante.
Para , temos:
E:
Substituindo por:
Temos:
E usando:
Nossa circunferência:
Se torna:
Elevando tudo ao quadrado:
Como:
Ficamos com:
Dividindo tudo por :
Então nossos limites serão:
Agora é só aplicar esses limites para calcular todas as nossas integrais dessa questão.
Passo 4
Podemos calcular a massa então:
Simplificando:
Começando pela integral de dentro em relação a e aplicando os limites de integração:
Integrando em agora:
Aplicando os limites, temos finalmente:
Passo 5
Note que temos uma simetria na figura em torno do eixo , ou seja, nossa figura é espelhada e tem as duas metades idênticas. Por causa da simetria, teremos e, portanto:
Pra calcular , primeiro vamos calcular o momento em relação ao eixo :
Substituindo nossa função densidade e fazendo:
Temos:
Integrando primeiro pela variável de dentro, tratando como constante e aplicando os limites de integração:
Finalmente integrando em :
Aplicando os limites, temos:
Então, temos:
Substituindo os valores que achamos: