Nos exercícios 1 a 5 calcular as derivadas laterais nos pontos onde a função não é derivável. Esboçar gráfico.
Passo 1
Opa!! Belezinha?!!
O enunciado nos deu essa função aqui:
Queremos calcular as derivadas laterais dessa funçãozinha e, em seguida, plotar o gráfico.
Para isso, temos que abrir o módulo da função, separando ela em dois casos:
Feito isso, agora podemos calcular as derivadas laterais no ponto x=3, que é justamente onde acontece o "vértice" do módulo!
Mas como fazemos isso?? Se liga no próximo passo!! 😉
Passo 2
Pessoal, a primeira coisa que podemos fazer é abrir essa função antes de começarmos a trabalhar na questão!
Se a função está definida em , então as derivadas à direita e a esquerda de em , denotadas por e são definidas por:
Uma fun��ão é derivável em um ponto, quando as derivadas à direita e à esquerda nesse ponto existem e são iguais.
Passo 3
Vamos aplicar essa definição na função da nossa questão no ponto crítico , onde ocorre o módulo:
Para , usamos .
Dessa forma, a nossa derivada fica:
Já para , usamos .
Assim, a nossa outra derivada fica:
Logo, como as derivadas laterais são diferentes, então podemos concluir que realmente não existe derivada em !!
Passo 4
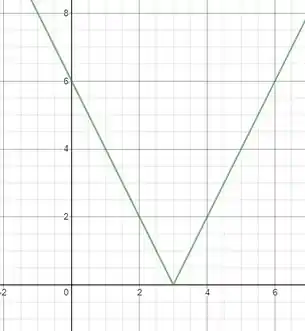
O gráfico é formado por duas retas que se encontram no ponto .
Para a reta sobe com inclinação , e para ela desce com inclinação , formando um , veja: