Jared Fogle, também conhecido como o “garoto propaganda do Subway”, pesava em , antes de perder mais em meses. Um gráfico mostrando a perde de peso, possivelmente dramática, é apresentado a seguir.
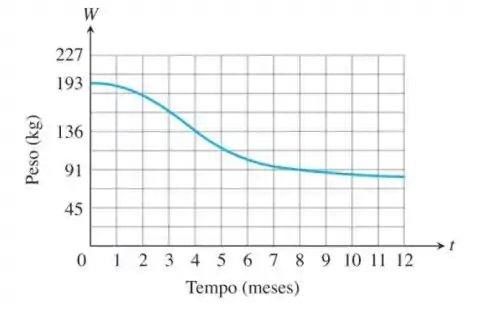
- Estime a taxa de perda de peso de Jared quando:
- Quando Jared perdeu peso mais rapidamente e qual é a taxa de perda de peso desse período?
- Utilize a técnica gráfica do exemplo 3 para traçar o gráfico da derivada do peso .
Passo 1
- A idéia para estimar a taxa de perda de peso é esboçar as retas tangentes aos pontos desejados, pois isso nos dá a derivada em cada ponto, ou seja, a taxa de variação do peso no gráfico.
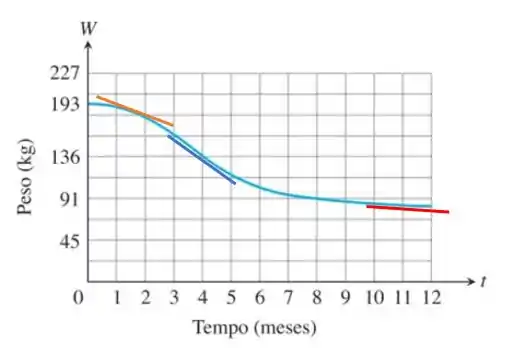
Passo 2
Observando as retas tangentes, devemos lembrar que a taxa de variação de uma função é o mesmo que o coeficiente angular dela, portanto, pra achar a variação, vamos marcar dois pontos próximos para poder saber a inclinação dela! Essas respostas vão ser aproximadas, já que estamos fazendo uma aproximação visual. O coeficiente da angular dessas retas vai ser, aproximadamente:
Passo 3
Essa resposta a gente vai obter do gráfico! O período em que ele perdeu peso mais rapidamente é aquele que tem a maior inclinação. Visualmente, a inclinação do gráfico no período de meses é a que parece ser mais inclinada! Por isso, no quarto mês foi o momento em que ele mais perdeu peso. Nesse momento, ele perdeu aproximadamente por mês, como vimos no item .
Passo 4
Pra esboçarmos o gráfico das derivadas, a gente vai traçar a tangente em vários intervalos do gráfico, para sabermos como ela se comporta. Mais uma vez, estamos mexendo com estimativa e esboço, então não necessariamente vai ser uma descrição perfeita! Vamos lá, fazendo aproximadamente a conta para cada mês. Já temos , e do item .
Entre e , a variação fica quase constante. Vamos colocar isso em um gráfico!
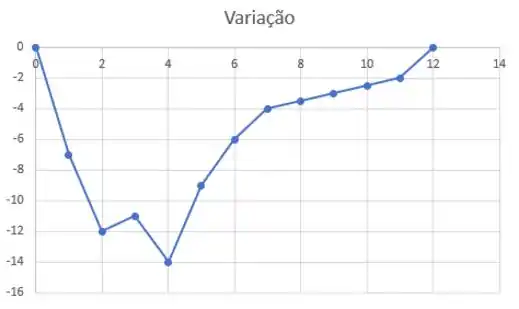
Resposta
Ei, a resposta está no passo a passo :)