19 - Centroide de um triângulo situa-se na interseção das medianas do triângulo Você deve recordar que o ponto dentro de um triângulo que se situe a um terço do caminho de cada lado em direção ao vértice oposto é o ponto onde as três medianas do triângulo se cruzam. Demonstre que o centroide está situado na interseção das medianas, mostrando que ele também está situado a um terço de distância de cada lado em direção ao vértice oposto. Para isso, siga os seguintes passos.
i) Coloque um lado do triângulo no eixo x como no item (b) da figura a seguir. Expresse dm em termos de L e dy.
ii) Use triângulos semelhantes para mostrar que L = (b/h) (h - y). Substitua essa expressão por L em sua fórmula para dm.
iii) Mostre que y = h/3.
iv) Faça o mesmo com os outros lados.
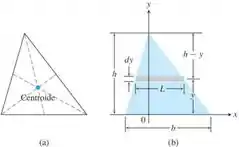
Passo 1
A massa horizontal da figura será , tendo que L é o comprimento do trângulo a uma distância de y acima da base localizada no eixo x. Desta forma utilizando triângulos semelhantes teremos que:
Desta forma:
Passo 2
Achar
Assim:
Resolvendo a integral teremos que
Substituindo teremos:
Logo:
Passo 3
Achar
Resolvendo a integral teremos:
Logo:
Passo 4
Sendo assim:
Assim fica demonstrado!
Resposta
Ei, a resposta está no passo a passo :)