Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 4.10 - Ex. 5
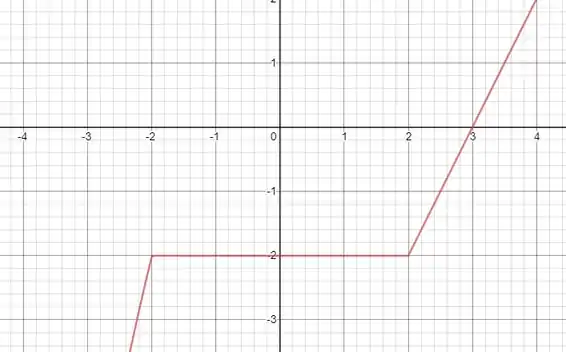
Nos exercícios 1 a 5 calcular as derivadas laterais nos pontos onde a função não é derivável. Esboçar gráfico.
Passo 1
Se a função está definida em , então as derivadas à direita e a esquerda de em , denotadas por e são definidas por:
Uma função é derivável em um ponto, quando as derivadas à direita e à esquerda nesse ponto existem e são iguais.
Passo 2
Vamos aplicar essa definição na função da nossa questão:
O gráfico da função é:
Resposta
Exercícios de Livros Relacionados
Calcule as derivadas à direita e à esquerda como limites para mostrar que a função não é derivável no ponto P.
Determine se a função definida por partes é derivável na origem g x = x 2 3 , x ≥ 0 x 1 3 , x0
Determine se a função definida por partes é derivável na origem f x = 2 x-1 , x ≥ 0 x 2 + 2 x+7 , x0
Jared Fogle, também conhecido como o “garoto propaganda do Subway”, pesava 193 k g em 1997 , antes de perder mais 108 k g em 12 meses. Um gráfico mostrando a perde de peso, possivelmente dramática, é
Nos exercícios 1 a 5 calcular as derivadas laterais nos pontos onde a função não é derivável. Esboçar gráfico. f x = x , s ex1 2 x - 1 , s ex ≥ 1