Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 7.8 - Ex. 4

Calcule ∬ S F ⋅ n d s   nos exercícios abaixo:

F ( x , y , z ) = ( x , y , z ) e S   é a superfície do sólido W , onde W = x , y , z ∈ R 3 x 2 + y 2 ≤ 1   e   x 2 + y 2 + z 2 ≤ 4 , com vetor normal n   exterior.

Passo 1

Bom galera, o exercício nos pede para calcular ∬ S F ⋅ n d s e nos dá as informações de que F ( x , y , z ) = ( x , y , z ) e que

S   : superfície do sólido W ,

com vetor normal n exterior.

W = x , y , z ∈ R 3 x 2 + y 2 ≤ 1   e   x 2 + y 2 + z 2 ≤ 4

Note que temos uma esfera e um cilindro, vamos desenhar pra ver qual a carinha do que queremos:

φ = π 6

cos ⁡ φ = 3 2

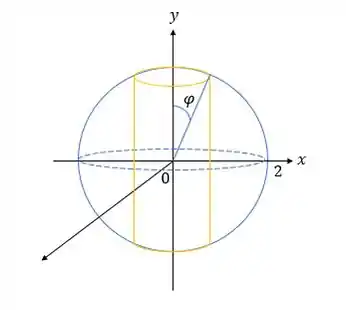
Nós temos duas equações: x 2 + y 2 + z 2 = 4 x 2 + y 2 = 1 . Como x 2 + y 2 = 1 então 1 + z 2 = 4 , logo z 2 = 3 e portanto z = ± 3 .

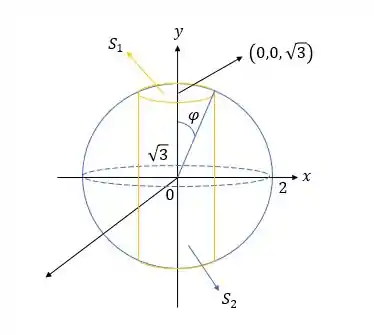
Também temos uma superfície S 3 , que é igual a S 1 só que a partezinha debaixo que não dá pra ver na figura, assim

S 1 e S 3 :

φ φ , θ = ( 2   s e n   φ cos ⁡ θ ,   2   s e n   φ   s e n   θ ,   2 cos ⁡ φ )

Com intervalo de 0 ≤ θ ≤ 2 π ≤ φ ≤ π 6 .

E

N φ φ , θ = ( 4   s e n 2 φ cos ⁡ θ ,   4   s e n 2 v a r p h i   s e n   θ ,   4 s e n φ cos ⁡ φ )  

Passo 2

Já podemos montar nossa integral:

∬ S F ⋅ n d s = ∬ S 3 F ⋅ n d s = 2 ⋅ ∬ S 3 F ⋅ n d s  

⇒ 2 ⋅ ∫ 0 2 π ∫ 0 π 6 ( 2   s e n   φ cos ⁡ θ ,   2   s e n   φ   s e n   θ ,   2 cos ⁡ φ ) ⋅ ( 4   s e n 2 φ cos ⁡ θ ,   4   s e n 2 v a r p h i   s e n   θ ,   4 s e n φ cos ⁡ φ ) d ϕ d θ = 2 ⋅ ∫ 0 2 π ∫ 0 π 6 ( 8   s e n 3 ϕ + 8   s e n   φ cos 2 ⁡ φ )   d φ d θ = 2 ⋅ ∫ 0 2 π ∫ 0 π 6 ( 8  sen φ ⁡ ) d φ d θ

Passo 3

Resolvendo a integral:

16 ⋅ ∫ 0 2 π [ - cos ⁡ φ ] 0 π 6 d θ = 16 ⋅ ∫ 0 2 π [ - cos ⁡ φ ] 0 π 6 = 16 ⋅ 2 π ⋅ - 3 2 + 1 = 32 π ⋅ - 3 2 + 32 π = - 16 3 π + 32   π

Passo 4

Agora S 2 :

φ θ , v = ( cos ⁡ θ ,       s e n   θ ,   v )

Com intervalo de integração de 0 ≤ θ ≤ 2 π - 3 ≤ v ≤ 3 .

E

N φ θ , v = ( cos ⁡ θ ,   s e n   θ ,   0 )  

Passo 5

Agora podemos montar nossa integral:

∬ S 2 F ⋅ n   d s = ∫ 0 2 π ∫ 0 3 cos 2 ⁡ θ + s e n 2 θ   d v d θ = 2 ⋅ 2 π ⋅ 3 = 4 3 π

Passo 6

Pronto, agora podemos juntar tudo numa soma:

∬ S F ⋅ n   d s = ∬ S 1 F ⋅ n   d s + ∬ S 2 F ⋅ n   d s + ∬ S 2 F ⋅ n   d s

Isso implica que

∬ S F ⋅ n   d s = - 16 3 π + 32   π + 4 3 π = 4 π ( 8 - 3 3 )

Resposta

4 π ( 8 - 3 3 )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja T a superfície do tetraedro limitado pelos planos coordenados e o plano x + y + z = 4 . Calcular I =∫ ∫ S y z d y d z + x z d z d x + x y d x d y = OndeS é a face da frente de TS é a face de T qu
Seja T a superfície do tetraedro limitado pelos planos coordenados e o plano x + y + z = 4 . Calcular I =∫ ∫ S y z d y d z + x z d z d x + x y d x d y = OndeS é a face da frente de TS é a face de T qu
1 . prove que Se a superficie S é dada na forma explicita por y = yx , z ,x , z ∈ R ' , onde R’ é a projeção sobre o plano xz e n denota a normal unitária de S com a componente y não negativa, obtemos
Calcule ∬ S F ⋅ n d s nos exercícios abaixo: F ( x , y , z ) = ( x , y , - 2 z ) e S é a esfera x 2 + y 2 + z 2 = 4 , com vetor normal n exterior.
Calcule ∬ S F ⋅ n d s nos exercícios abaixo: F ( x , y , z ) = ( z 2 - x , - x y , 3 z ) e S é a superfície do sólido limitado por z = 4 - y 2 , x = 0 , x = 3 e o plano x y , com vetor normal n exteri