Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 6.5 - Ex. 42
Calcule a força do fluido em um lado de uma placa com a forma de um triângulo retângulo com lados de 3, 4 e 5 pés. Com a placa estiver no fundo de uma piscina cheia de água a uma profundidade de 6 pés em sua borda de 3 pés, e com uma inclinação de 60° em relação ao fundo da piscina.
Passo 1
A primeira coisa que precisamos entender é o trabalho não é igual para cada altura do triangulo. A cada altura temos uma pressão de água diferente. Então precisamos fazer uma diferencial levando em conta essa altura e pressão.
Passo 2
Vamos relembrar algumas coisas que sabemos
Estamos usando lb então vamos usar em lb também
Passo 3
Vamos desenhar para entender o que está acontecendo
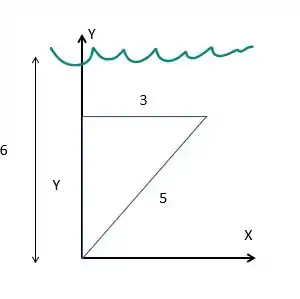
Beleza. Então temos um triangulo mergulhado e podemos deixar ele nesse formato para facilitar as contas. Estamos num problema mais evoluído. Esse triangulo não está em pé certinho. Ele faz um ângulo com o chão. Então vamos tratar esse como
Temos que calcular a área desse triangulo por integração. E como só temos ferramentas para fazer esse cálculo com UMA ÚNICA VARIAVEL. Então Podemos usar essa reta da hipotenusa para isso :
E também podemos definir a profundidade como sendo
Pronto já temos tudo. Vamos apenas descobrir como se comporta esse . Bem, ele é uma altura. E está inclinado a . Logo não seria nada mal a gente dizer que
E de fato é assim que nosso funciona. Vamos Então juntar tudo nada integral
Show. Estamos dentro do que podemos gastar. Beleza terminamos por aqui. Te encontro na próxima resolução. Até mais : )