Calcule a função f x = x 2 - 2 x 1000 Para x = 1 ,0,8 ,0,6 ,0,4 ,0,2 ,0,1 e0,05 e faça uma conjectura sobre o valor de lim x → 0 ⁡ x 2 - 2 x 1000 Calcule f ( x ) para x = 0,04 ,0,02 ,0,01 ,0,005 ,0,003 ,0,001 . Faça uma nova conjectura.

lim x → 0 ⁡ x 2 - 2 x 1000 = 0 lim x → 0 ⁡ x 2 - 2 x 1000 = - 0,001

Enunciado

Eaee, belezinha?? Bom... o enunciado nos dá a seguinte função:

Queremos calcular para os seguintes valores de :

Para isso, basta substituirmos na expressão citada.

Depois vamos analisar os resultados e analisar uma comparação com o seguinte limite:

Por fim, vamos refazre tudo novamente, mas com os seguintes valores de :

Vamos calcular primeiro e os valores seguintes de a gente apresenta em uma tabela (para comparar melhor com o limite):

Agora, para os demais valores de , temos:

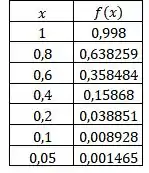
Mas o que isso tem a ver com o limite dado???

Bom... perceba que o limite é para quando se aproxima de .

Perceba que os valores de da tabela vão se aproximando cada vez mais de também!!!

E, quanto mais se aproxima de , mais se aproxima de também!!

Com isso, podemos concluir que:

Agora para os outros valores de , faremos de forma análoga:

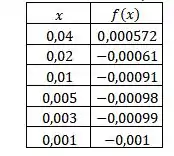
Analisando a tabela, podemos ver que quanto mais se aproxima de , mais se aproxima de , portanto: