Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.2 - Ex. 44

Encontre as assíntotas verticais da função

Confirme sua resposta da parte (a) fazendo o gráfico da função

Passo 1

Olá, meu nobre amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.

Aqui o que iremos fazer é encontrar as assintotas verticais da função dada.

Para encontrar as assíntotas da função precisamos calcular valores de tal que

Passo 2

Então,

Isso acontece quando o denominador de tende a zero, é um valor tão pequeno que quando divide a função ela acaba ‘explodindo’, então podemos calcular os valores de igualando o denominador a zero e encontrando os valores de correspondentes. Então

Esboçando o gráfico da função com o auxilio do GeoGebra, ficamos com

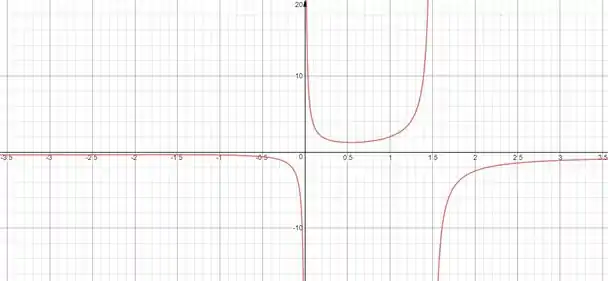
E podemos confirmar os resultados obtidos de forma algébrica

Resposta

são as assíntotas verticais da função

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a função R cujo gráfico é mostrado a seguir, diga quem são: l i m x → 2R ( x ) l i m x → 5R ( x ) l i m x →- 3 -R ( x ) l i m x →- 3 +R ( x ) As equações das assíntotas verticais

Use um gráfico para estimar as equações de todas as assíntotas verticais da curva y = tan ⁡ 2 sin ⁡ x ,- π ≤ x ≤ π Encontre então as equações exatas dessas assíntotas.

Para a função f cujo o gráfico é dado, diga quem são a lim x → 2 ⁡ f ( x ) b lim x → - 1 - ⁡ f ( x ) c lim x → - 1 + ⁡ f ( x ) d lim x → ∞ ⁡ f ( x ) e lim x → - ∞ ⁡ f ( x ) f A se q u a ç õ e sd a sa

Para a função g cujo o gráfico é dado, determine o que se pede a lim x → ∞ ⁡ g ( x ) b lim x → - ∞ ⁡ g ( x ) c lim x → 3 ⁡ g ( x ) d lim x → 0 ⁡ g ( x ) e lim x → - 2 + ⁡ g ( x ) f A se q u a ç õ e sd

( a ) O gráfico de y = f ( x ) pode interceptar uma assíntota vertical? E uma assíntota Horizontal? Ilustre com gráficos. ( b ) Quantas assíntotas horizontais pode ter o gráfico de y = f ( x ) ? Ilust