Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.2 - Ex. 56
- Use evidências numéricas e gráficas para fazer uma conjectura sobre o valor do limite
- A que distância de 1 deverá estar para garantir que a função da parte (a) esteja a uma distância de 0,5 de seu limite?
Passo 1
Fala aí, meus amores!
Aqui temos que calcular o seguinte limite pelo gráfico e numericamente:
Mas se a gente substituir na expressão vamos ter uma indeterminação
Então vamos ter que manipular e simplificar essa equação pra achar o resultado. Já vou dar uma dica! Repara que temos uma diferença de cubos no numerador e isso aí a gente pode fatorar!
Depois vamos comparar esse resultado com o que a gente visualizar no gráfico.
No item (b) a gente quer saber o quão perto precisa estar de 1 pra que o a função esteja a uma distância de 0,5 do seu limite. Calma, não se assusta! A simplesmente vai olhar no gráfico quais pontos estão a essa distância.
Bom, mas vamos primeiro pro passo 2, calcular o nosso limite.
Passo 2
Vamos lembrar dessa maravilhosa fatoração clássica que temos aqui:
Aplicando no numerador da nossa expressão:
E agora a gente vai dar uma forçada de barra aqui e dizer que esse primeiro termo é uma diferença de quadrados!
Meu deus, Iasmin, mas de onde vem uma ideia dessa?
Vem do denominador. A gente precisa se livrar dele pra acabar com a indeterminação. E como tem um ali e , a gente pode reescrever assim:
Agora podemos aplicar essa outra fatoração aqui:
Na nossa expressão:
OPAAAA! NUM É QUE APARECEU UM TERMO IGUALZINHO AO DENOMINADOR!
Vamos substituir isso tudo no nosso limite!
E como , ele nunca vai ser igual a 1, então podemos simplificar esse termo (é tudo amarradinho aqui!)
E nosso limite se torna
Uhuuulll!!! Agora vamos pro gráfico!
Passo 3
Bom, pra traçar uma função dessa, a gente realmente vai ter que usar um software, não vai ter jeito.
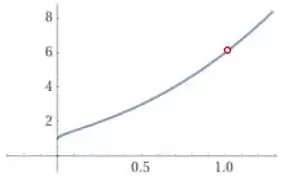
Por conta desse denominador que não pode ser zero, a função tem uma descontinuidadezinha ali no
Mas isso não influencia o nosso limite, porque o limite não é o valor da função, mas o valor que ela se aproxima quando se aproxima de 1.
E quando se aproxima de 1, se aproxima de 6, então:
Uhuuull, achamos o mesmo valor!
Passo 4
Agora, no item (b) a gente quer saber o quão perto precisa estar de 1 pra que o a função esteja a uma distância de 0,5 do seu limite.
Bom, se o limite que calculamos é
queremos que:
Agora basta encontrarmos no gráfico da função valores de tal que e .
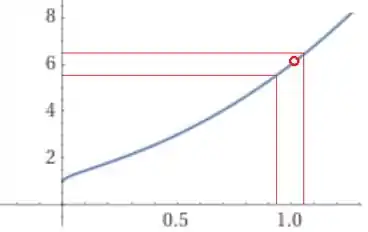
Analisando o gráfico, podemos concluir que
Porém, o problema nos pede a que distância devemos estar de 1, então, basta fazermos o seguinte cálculo para os dois valores de encontrados
Então, para garantir que a função esteja a 0,5 de distância do valor do limite calculado, basta que esteja a 0,07 de distância de 1
Resposta
- deve estar a 0,07 de distância de 1