Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 8.Exercícios Práticos - Ex. 29 b

Calcule as integrais. B) Usando substituição trigonométrica

Passo 1

Já que temos que usar substituição trigonométrica, nada melhor que visualizar o triângulo retângulo que dá origem à nossas substituições.

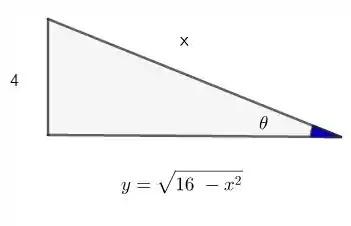
Vamos começar as contas então, blz?

y = 4   s i n θ ⟹ d y = 4   c o s θ  

Daí,

∫ y 16 - y 2   d y = 4   ∫     s e n θ   c o s θ   d θ 16 - 4 2 s e n 2 θ   = 4   ∫     s e n θ   c o s θ   d θ 16 ( 1 - s e n 2 θ )   = 4 4 ∫     s e n θ   c o s θ   d θ 1 - s e n 2 θ  

Passo 2

Usando a identidade trigonométrica s e n 2 x + cos 2 ⁡ x = 1 temos que 1 - s e n 2 x = cos 2 ⁡ x

Daí,

4 4 ∫     s e n θ   c o s θ   d θ 1 - s e n 2 θ = ∫   s e n θ   c o s θ   d θ cos 2 ⁡ θ =   ∫     s e n θ   c o s θ c o s θ     d θ = ∫ s e n θ   d θ = - c o s θ + C

Passo 3

Olhando para o nosso triângulo e sabendo que cosseno é cateto adjacente pela hipotenusa,

c o s θ = 16 - y 2 4    

Passo 4

Sendo assim, nossas contas ficam

∫ y 16 - y 2   d y =   ∫ s e n θ   d θ =   c o s θ + C = -   16 - y 2 4 + C    

Resposta

∫ y 16 - y 2   d y =   -   16 - y 2 4 + C    

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral indefinida: ∫ 5 x + 4 x 3 x 2 + 1d x
Calcule a integral indefinida: ∫ 1 - 4 t 2 3 2 d t
Calcule a integral indefinida: ∫ 1 + x 2 x 3d x
Calcule a integral indefinida: ∫ x + 1 2 x 2 + 1 d x
Calcule a integral indefinida: ∫ x 2 2 - x 2d x