Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 5.8 - Ex. 33

Calcule a integral definida

int_0^1 s e n ( pi x ) c o s ( pi x ) d x

Passo 1

Propriedade de integral

int_b^a f (x) d x = F (a) - F (b)

int_b^a f (x) + g (x) d x = int_b^a f (x) d x + int_b^a g (x) d x

int_()^() x^n = (x)/(n + 1)^(n + 1)

Passo 2

Agora está na hora de usar tudo o que praticamos de integrais e identidades trigonométricas

Vou usar a seguinte identidade

s e n (pi x) cos (pi x) = (s e n 2 pi x)/(2)

A integral fica

int_0^1 s e n (pi x) cos (pi x) d x = int_0^1 (s e n 2 pi x)/(2) d x

Olha so como ficou mais fácil, transformamos dois termos em um apenas. E integral de função trigonométrica básica igual nos temos é moleza

Passo 3

int_0^1 (s e n 2 pi x)/(2) d x = - ((c o s 2 pi x)/(4 pi)|_(x = 0)^1

- (1)/(4 pi) ( cos 2 pi - c o s 0 )

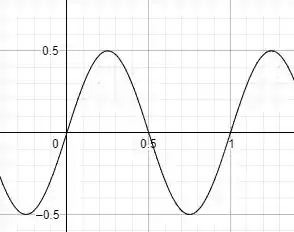
Olha que coisa cos 2 pi = cos 0 . Então essa integral é zero. Isso acontece porque integramos numa região, onde a área positiva era igual a área negativa

E ao somar elas se anulam . Podemos observar isso na imagem abaixo da nossa função

(s e n 2 pi x)/(2)

Resposta

int_0^1 s e n (pi x) cos (pi x) d x = 0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule as integrais indefinidas nos Exercícios 1-16 usando as substituições dadas para reduzir as integrais à forma padrão ∫ x sen ⁡ ( 2 x 2 ) d x , u = 2 x 2
Calcule as integrais indefinidas nos Exercícios 1-16 usando as substituições dadas para reduzir as integrais à forma padrão ∫ 3 x + 2 3 x 2 + 4 x 4 d x , u = 3 x 2 + 4 x
Calcule as integrais indefinidas nos Exercícios 1-16 usando as substituições dadas para reduzir as integrais à forma padrão ∫ 9 r 2 1 - r 3 d r , u = 1 - r 3
Calcule as integrais indefinidas nos Exercícios 1-16 usando as substituições dadas para reduzir as integrais à forma padrão ∫ cossec 2 ⁡ 2 θ cotg ⁡ 2 θ d θ a) u = cotg ⁡ 2 θ b) u = cossec ⁡ 2 θ
Calcule as integrais nos Exercícios 17-66. ∫ 1 x 1 + x 2 d x