Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 5.5 - Ex. 67
Calcule a integral definida, se ela existir.
Passo 1
Blzinha?
O problema nos pede para calcular a seguinte integral:
Se ele existir.
Antes de sair calculando é sempre importante tentarmos entender a nossa função, nesse caso temos uma limitação em nossa função, pois não podemos dividir por .
A integral é a área abaixo da curva, desde que a função seja contínua, ou seja, sem saltos, quebras e picos para o intervalo analisado!
Passo 2
Se observarmos o domínio da função que está no integrando podemos perceber que ela só apresenta um “problema” para o valor de . Como nosso intervalo de integração engloba esse ponto, a nossa integral não existirá ou vai divergir. O que faz sentido, haja vista que a nossa integral indica uma área sob a curva e a nossa curva para o intervalo dado é representada por
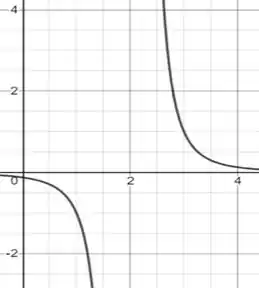
Percebe como a linha da função se rompe? Então não podemos calcular esta integral para esse limite, mas se o limite fosse ou , aí sim poderíamos calcular, pois nestes intervalos a função é contínua!
Resposta
A integral vai divergir