Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 5.5 - Ex. 45

Calcule a integral indefinida. Ilustre e verifique se sua resposta é razoável fazendo um gráfico da função e de sua antiderivada (tome C = 0 ) .

∫ 3 x - 1 3 x 2 - 2 x + 1 4 d x

Passo 1

Fala aí! tudo certinho?

Nesse problema temos que calcular a integral:

∫ 3 x - 1 3 x 2 - 2 x + 1 4 d x

E verificar o resultado ilustrando o gráfico de f e de sua antiderivada com C = 0 .

Tem ideia de como fazemos isso?

Perceba que na forma como está a função da integral não vamos saber calcular essa integral.

Então para facilitar nossa vida podemos usar o método de substituição.

Esse método consiste em fazer uma mudança de variáveis do tipo:

∫ f x d x → ∫ g u d u

A ideia é substituir parte de f x para chamar de u e derivar u em relação a x para obter d u e montar nossa integral.

Encontrar a substituição correta depende da nossa sagacidade em conseguir visualizar como podemos simplificar a integral... então quanto mais questões fizermos, melhor vai ser.

Veja só!

Passo 2

Nossa função de integração é dada por:

f x = 3 x - 1 3 x 2 - 2 x + 1 4

Assim podemos chamar 3 x 2 - 2 x + 1 de u .

u = 3 x 2 - 2 x + 1

Derivando u em relação a x .

d u d x = 6 x - 2 = 2 3 x - 1

Isolando d x em um lado da igualdade:

d x = 1 2 3 x - 1 d u

Com isso, substituindo 3 x 2 - 2 x + 1 e d x na integral do problema, vamos obter:

∫ 3 x - 1 3 x 2 - 2 x + 1 4 d x → ∫ 3 x - 1 u 4 1 2 3 x - 1 d u

Perceba que podemos simplificar 3 x - 1 .

1 2 ∫ 1 u 4 d u

1 2 ∫ u - 4 d u

Tranquilo até aqui?

Passo 3

Viu que a gente conseguiu transformar uma integral extremamente difícil em uma integral bem mais simples? Para resolvê-la basta aplicarmos a regra da potência.

∫ a x n d x = a x n + 1 n + 1 + C

Veja só!

1 2 ∫ u - 4 d u = 1 2 u - 4 + 1 - 4 + 1 + C = - 1 2 u - 3 3 + C

1 2 ∫ u - 4 d u = - 1 6 u 3 + C

Não podemos deixar o resultado em função de u , então voltamos para x .

∫ 3 x - 1 3 x 2 - 2 x + 1 4 d x = - 1 6 3 x 2 - 2 x + 1 3 + C

Show?

Passo 4

Para conferir nossa resposta, vamos plotar em um mesmo gráfico a função do integrando e sua integral (com C = 0 ). Dessa forma, obteremos

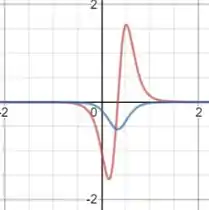
Em vermelho temos f x e em azul a integral de f x .

A integral de uma função pode ser interpretada como a área abaixo da curva dessa função. Perceba que f x é negativa até x = 1 3 e a partir desse ponto f x fica positiva. esse comportamento reflete na curva em azul que é decrescente até x = 1 3 e quando f fica positiva, a curva azul passa a ser crescente.

É isso! O que achou? Responde Aí!

Resposta

∫ 3 x - 1 3 x 2 - 2 x + 1 4 d x = - 1 6 3 x 2 - 2 x + 1 3 + C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Avalie a integral fazendo a substituição fornecida. ∫ x 3 x 4 - 5 d x , u = x 4 - 5
Avalie a integral fazendo a substituição fornecida. ∫ sen 2 ⁡ θ cos ⁡ θ d θ , u = sen ⁡ θ
Calcule a integral indefinida. ∫ y 2 4 - y 3 2 3 d y
Calcule a integral indefinida. ∫ 3 x - 2 20d x
Avalie a integral indefinida.int cos ((pi t)/(2)) d t