Calcule a integral indefinida. Ilustre e verifique que sua resposta é razoável fazendo o gráfico da função e de sua primitiva (tome C=0).

Vamos aplicar o método da substituição para solucionarmos o problema,

A integral fica:

Logo,

Tomando C como 0 e fazendo o gráfico dessa integral, temos que

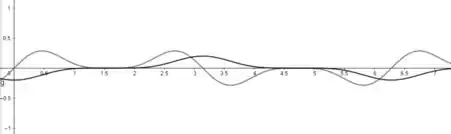
A curva acima é a da integral f(x), também representada pela cor acinzentada, e abaixo é a de F(x), de cor preta. Podemos perceber que onde f intercepta o eixo x é equivalente a , então f muda de positivo para negativo e F tem um máximo local. Além disso, f e F são periódicos no período , portanto, em x = 0 e x = , f muda de negativo para positivo e F tem um mínimo local.