Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 5.5 - Ex. 51
Calcule a integral indefinida. Ilustre e verifique que sua resposta é razoável fazendo o gráfico da função e de sua primitiva (tome ).
Passo 1
E aí, galera! Tudo certinho 😎?
Nesse problema precisamos calcular a integral indefinida
e, feito isso, precisamos analisar o gráfico da função e da primitiva encontrada (com a constante de integração igual a zero) para verificar se a resposta faz sentido.
Em um primeiro momento, essa integral não se parece com nenhuma das presentes na Tabela de Integrais Indefinidas, né?
🤔 Bem, então como resolvemos essa questão?
Utilizando a Regra da Substituição para transformar essa integral em uma outra integral existente na Tabela, cujo valor sabemos calcular.
Saca só o que a regra diz: Se definirmos a função derivável como uma variável , ou seja, , e se a função for contínua em seu domínio então vale que
desde que a imagem de esteja contida no domínio de
💡 Vamos relembrar de algumas propriedades das integrais indefinidas que vão nos ajudar a resolver essa questão.
- A integral indefinida do produto entre uma constante e uma função é o produto entre a constante e a integral indefinida da função.
- A integral indefinida da exponencial é ela mesma:
Precisamos lembrar também da derivada da função cosseno:
Temos tudo o que precisamos. Bora lá 😊!
Passo 2
Analisando com calma o integrando da integral
podemos ver que, se
e
então
e, além disso, derivando em relação à variável , temos que
ou seja
Sendo assim, observe que
ou seja,
Sendo assim, pela Regra da Substituição temos que a integral do enunciado pode ser reescrita como
onde
Mas observe que essa integral da direita, em função da variável , nós sabemos calcular né? Temos que
Logo,
ou seja, temos que
onde é uma constante qualquer.
Passo 3
Ainda não terminamos, né? A igualdade
não é a resposta final, pois precisamos reverter a mudança de variável que fizemos ao assumir
Fazendo isso, vamos ter que
ou seja, a integral do enunciado é dada por
Passo 4
Assumindo a constante de integração como sendo zero, conforme pedido no enunciado, então encontramos que uma primitiva para a função
é dada por
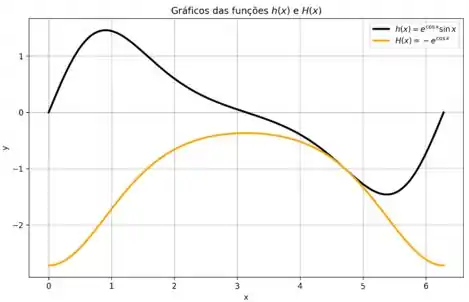
Utilizando uma ferramenta gráfica para a construção dos gráficos e considerando que as funções são periódicas, com período , então os gráficos das funções no intervalo são dados na imagem abaixo.
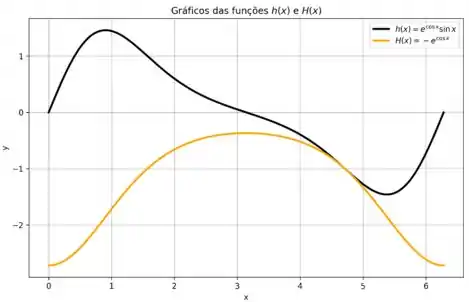
Como a integral de uma função representa a área acumulada sob a curva, de forma que quando a curva assume valores negativos temos que o valor total acumulado para a área diminui, então observe que:
- Quando , está aumentando, indicando que a área acumulada sob a curva é positiva.
- Quando , está diminuindo, indicando que a área acumulada é negativa.
- Os pontos onde são pontos críticos para , podendo ser máximos ou mínimos.
Resposta
A integral indefinida é dada por:
e um esboço para os gráficos pode ser visto na imagem abaixo.
