Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 5.5 - Ex. 49
Calcule a integral indefinida. Ilustre e verifique se sua resposta é razoável fazendo o gráfico da função e de sua primitiva (tome ).
Passo 1
Opa, bora resolver esse problema! Devemos calcular a seguinte integral:
O problema aqui é que a gente não consegue resolver ela direto usando as primitivas. Então vamos usar uma técnica de integração chamada Regra da Substituição!
Mas o que é a integração por substituição?
Lembra que a integral é a operação contraria da primitiva? Então temos que ela deve ser realmente o inverso da regra da cadeia. De acordo com a regra da cadeia para a derivada temos:
Na integração por substituição, pegamos uma expressão da forma e encontramos sua primitiva.
A integração por substituição nos ajuda a simplificar uma expressão confusa, transformando a função "interna" na variável. Então temos que encontrar o resultado dessa integral:
Para simplificar essa integral, colocamos uma nova variável tal que . Isso significa que .
Substituindo essas expressões na integral, obtemos:
Depois de integrar em relação a , obtemos . Finalmente, substituímos de volta por para obter a resposta na variável original .
Então vamos fazer uma mudança de variável para encontrar o valor dessa integral, vemos que temos um, podemos então usar a mudança de variável:
Dica: o melhor é aquele que simplifica a nossa integral! Além disso a derivada de deve estar dentro da integral (como uma regra da cadeia inversa).
Derivamos:
Fazendo a substituição , a integral fica:
Passo 2
Agora integramos, e para isso podemos usar o auxílio de uma tabela de primitivas:
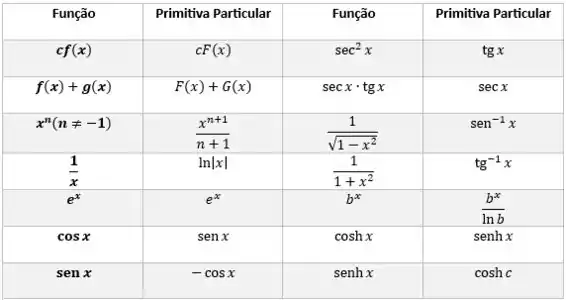
Vamos aplicar a primitiva da potência:
Voltando a variável original:
Passo 3
Agora a gente deve fazer o gráfico da função e da sua primitiva:
A função:
A primitiva:
Tomando , em vermelho fazemos o gráfico da função e em azul o de sua primitiva:
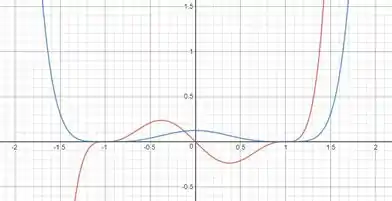
Como a função se comporta como a derivada de sua primitiva, note que quando a curva vermelha é positiva, a curva é crescente, enquanto na região que a curva vermelha é negativa, a curva azul é decrescente. Além disso, nos pontos que a curva vermelha se anula, a curva azul tem tangente horizontal.