Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 5.3 - Ex. 53
Calcule a integral e interprete-a como uma diferença de áreas. Ilustre com um esboço
Passo 1
Falaee, belezinha??? Bom... queremos calcular a seguinte integral:
Em seguida devemos interpretá-la como uma diferença de áreas e ilustrar com um esboço.
Para isso, é interessante sabermos da Parte 2 do Teorema Fundamental do Cálculo, para exemplificar imagine que você está em uma montanha-russa representando a função contínua . Conforme você viaja da posição até , uma função (que é a primitiva de ) conhece a altura da montanha-russa em qualquer ponto.
O Teorema Fundamental do Cálculo diz que a área total coberta nessa viagem, ou seja, a integral de de até , é simplesmente a diferença entre a altura final e a inicial.
Em outras palavras, a integral da função é a diferença das alturas nas extremidades do intervalo, tornando os cálculos muito mais simples! Dessa forma temos:
Se for contínua em (como uma montanha russa, que não pode ter saltos e quinas) então:
Onde é qualquer primitiva de , isto é, uma função tal que .
Também usaremos a seguinte tabela:
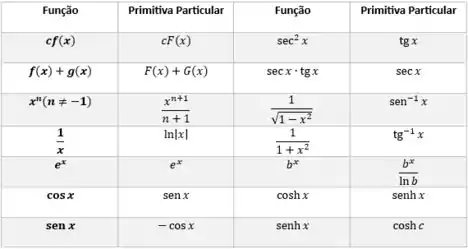
Onde usaremos a primitiva do polinômio:
Agora estamos que prontos bora aplicar!! 😉
Passo 2
Primeiro, vamos calcular a integral analiticamente, pra isso, é só integrarmos a função do mesmo jeito que a gente integra .
Então, aplicando o Teorema Fundamental do Cálculo, temos:
Avaliando os limites da integração:
Passo 3
Agora, podemos interpretar o resultado obtido da seguinte maneira
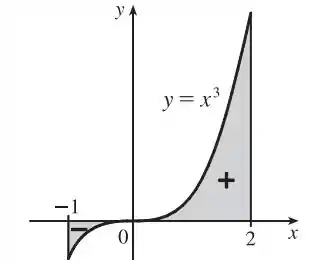
Em outras palavras, a integral que encontramos no Passo 2 nada mais é do que a soma dessas duas áreas aí de cima.
Mas perceba que uma está no lado negativo. Assim, o valor da integral pode ser entendido como a área da região positiva menos a área da região negativa!!
Entendeu direitinho?? Responde aee😉