Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 5.3 - Ex. 52

Calcule a integral e interprete-a como uma diferença de áreas. Ilustre com um esboço

∫ π 4 5 π 2 sin ⁡ x d x

Passo 1

Pessoal, nessa questão queremos calcular a seguinte integral:

∫ π 4 5 π 2 sin ⁡ x d x

Sabemos que uma integral definida é dada por:

∫ a b f x d x = F b - F ( a )

Sendo F ( x ) uma função que quando derivada resulta em f ( x ) :

f x = F ' ( x )

Sabemos também que a integral representa a área abaixo da função, de forma que se a função está acima do eixo x esse valor é positivo e se a função está abaixo do eixo x , encontramos a área, mas com um valor negativo.

Passo 2

Essa integral é bem simples, não é mesmo? Então podemos calcular diretamente da seguinte maneira

∫ a b f x d x = F x b a

A função que quando derivada resulta no seno é o menos cosseno, logo:

∫ π 4 5 π 2 sin ⁡ x d x = - cos ⁡ x π 4 5 π 2

= - cos ⁡ 5 π 2 - - cos ⁡ π 4

= 0 + 2 2 = 2 2

Passo 3

Podemos interpretar o resultado obtido da seguinte maneira:

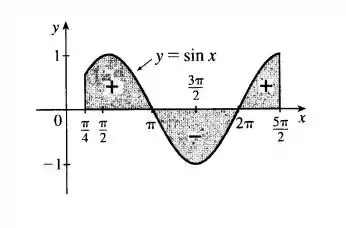
Perceba que a área que está abaixo do eixo x é calculada de forma negativa e a área que está acima do eixo x é calculada de forma positiva.

Resposta

∫ π 4 5 π 2 sin ⁡ x d x = 2 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a área das regiões delimitadas pelas curvas e retas y 2 = 4 x , y = 4 x - 2
Determine a área da região cortada do primeiro quadrante pela curva x 1 2 + y 1 2 = a 1 2
Determine a área entre a curva y = 1 x e o eixo x de x = 10 até x = 20 é a mesma área entre a curva e o eixo x de x = 1 até x = 2 .
Determine a área total da região delimitada pela curva = s e n x , y = c o s x0 ≤ x ≤ 3 π 2
Determine a área entre a curva y = 1 x e o eixo x de k a até k b é a mesma área entre a curva e o eixo x de x = a até x = b . ( 0ab , k0 ).